Bảng lượng giác và các công thức lượng giác Toán học 9

Bảng lượng giác là một bài lý thuyết trong chương I hình học Toán 9 nghiên cứu về Hệ thức lượng trong tam giác vuông. xin được gửi tới các bạn bài lý thuyết và các dạng bài tập đầy đủ và chi tiết nhất về bảng lượng giác lớp 9. Hy vọng qua bài viết này sẽ giúp các bạn ghi nhớ hơn về các bảng lượng giác cơ bản và bảng lượng giác đặc biệt!

A. Tóm tắt lý thuyết toán 9 bảng lượng giác

1. Cấu tạo của một bảng lượng giác lớp 9

- Theo cuốn sách "Bảng số với bốn chữ số thập phân" của tác giả V.M. Bra-đi-xơ thì bảng lượng giác được bao gồm có ba bảng đó là bảng VIII, bảng IX và bảng X. Trong đó các bảng đều được thành lập dựa trên một tính chất là nếu tổng hai góc bất kỳ trong một tam giác bằng \(90^0\) thì \(sin\alpha =cos\beta \), \(cos\alpha =sin\beta \), \( tan\alpha =cot\beta\), \(cot\alpha =tan\beta \).

=> Bảng VIII được tạo bởi 15 hàng và 16 cột ghi các giá trị của sin và cos của một số góc có số đo độ nhỏ hơn \(90^0\). Đồng thời, khi biết sin và cos của một góc bất kỳ, có thể tra theo bảo để tìm ra được độ lớn góc đó. Trong cấu tạo của bảng VIII, có:

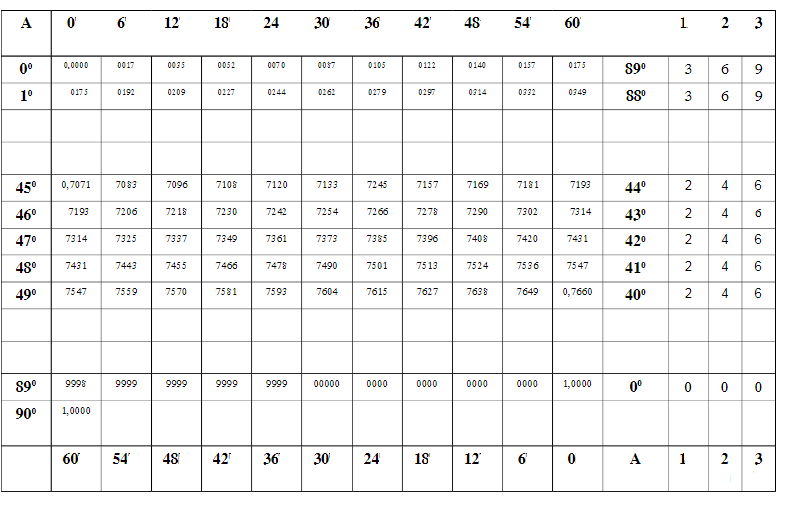
+ Hai vị trí là cột thứ nhất và cột số 13 là các số nguyên độ. Theo thứ tự từ trên xuống dưới, ở vị trí cột thứ nhất ghi các số đo độ được sắp xếp theo một thứ tự lớn dần từ \(0^0\) đến \(90^0\) và ngược lại từ cột thứ 13 là sắp xếp theo một thứ tự giảm dần.

+ Ba cột cuối cùng biểu diễn một số giá trị có chức năng hiệu chỉnh trong các trường hợp góc sai khác 1', 2', 3'.

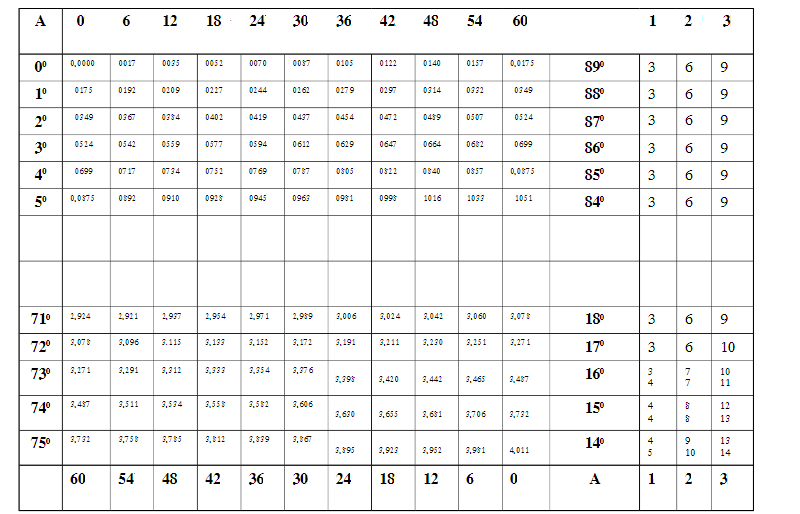
=> Bảng IX được tạo bởi 15 hàng và 16 cột ghi các giá trị tan của một số góc có số đo độ từ \(0^0\) đến \(76^0\) và giá trị cot của một số góc có số đo độ từ \(14^0\) đến \(90^0\). Đồng thời, khi biết tan và cot của một góc bất kỳ, có thể tra theo bảo để tìm ra được độ lớn góc đó. Trong cấu tạo của bảng VIII, có:

+ Hai vị trí là cột thứ nhất và cột số 13 là các số nguyên độ. Theo thứ tự từ trên xuống dưới, ở vị trí cột thứ nhất ghi các số đo độ được sắp xếp theo một thứ tự lớn dần từ \(0^0\) đến \(90^0\) và ngược lại từ cột thứ 13 là sắp xếp theo một thứ tự giảm dần.

+ Ba cột cuối cùng biểu diễn một số giá trị có chức năng hiệu chỉnh trong các trường hợp góc sai khác 1', 2', 3'.

- Bảng X ghi các giá trị tan của một số góc có số đo độ từ \(76^0\) đến \(89^059'\) và giá trị cot của một số góc có số đo độ từ \(1'\) đến \(14^0\). Đồng thời, khi biết tan và cot của một góc bất kỳ, có thể tra theo bảo để tìm ra được độ lớn góc đó.

2. Dùng bảo lượng giác như thế nào? 

a, Với một góc có số đo nhỏ hơn \(90^0\) cho trước, hãy tính tỉ số lượng giác của nó:

Bước 1: Với sin và tan, muốn tìm số độ thì tra số độ ở vị trí cột thứ nhất, còn đối với cos và cot thì tra số độ ở cột thứ 13.

Bước 2: Với sin và tan, muốn tìm số phút thì tra số phút ở vị trí hàng thứ nhất, còn đối với cos và cot thì tra số phút ở hàng cuối.

Bước 3: Giá trị sẽ là giao cột số phút với giao hàng số độ.

b, Với một góc có số đo độ nhỏ hơn \(90^0\) cho trước và tỉ số lượng giác cho trước, hãy tính số đo độ

B. Một số bài tập toán 9 bảng lượng giác

Bài 1: Dựa vào các bảng lượng giác như bảng VIII, bảng IX, bảng X hoặc dùng máy tính bỏ túi để tính một số góc có số đo độ nhỏ hơn \(90^0 \) sau:

a, \(sinx=0,5446\)

b, \(cos x=0,4444\)

c, \(tanx=1,1111\)

Hướng dẫn giải bằng máy tính bỏ túi:

a, \(sinx=0,5446\) => \(x=33^0\)

b, \(cos x=0,4444\) => \(x=63^047'\)

c, \(tanx=1,1111\) => \(x=48^0\)

Bài 2: Dựa vào các bảng lượng giác như bảng VIII, bảng IX, bảng X hoặc dùng máy tính bỏ túi để tính các giá trị lượng giác của một số góc sau:

a, \(sin39^013'\) 

Trả lời: \(sin39^013'\) \(\approx 0,6323\)

b, \(cos52^018'\)

Trả lời: \(cos52^018'\) \(\approx 0,6115\)

c, \(tan 13^020'\)

Trả lời: \(tan 13^020'\) \(\approx 0,2370\)

d, \(cot 10^017'\) 

Trả lời: \(cot 10^017'\) \(\approx 0,5118\)

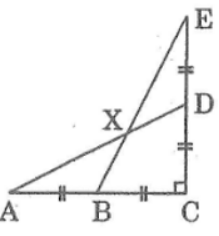
Bài 3: Cho hình vẽ bên dưới, biết rằng góc \(\widehat{ACE}\) có độ lớn bằng \(90^0\), độ dài của các cạnh \(AB,BC,CD,DE\) là bằng nhau và bằng 2cm. Hỏi:

a, Các cạnh \(AD,BE\) có độ dài là bao nhiêu?

b, Độ lớn của góc \(\widehat{DAC}\), \(\widehat{BXD}\)?

a, Theo dữ kiện đề bài, ta có: \(AC=AB+BC\) = 2 + 2 = 4 (cm)

Trong tam giác ACD có góc \(\widehat{C}=90^0\),áp dụng định lý Py-ta-go ta có:

\(AD^2=AC^2+CD^2=4^2+2^2=20\) => \(AD=\sqrt{20}=2\sqrt{5}\)

Ta lại có: \(CE=CD+DE = 2+2=4 (cm)\)

Trong tam giác BEC có góc \(\widehat{C}=90^0\),áp dụng định lý Py-ta-go ta có:

\(BE^2=BC^2+CE^2=4^2+2^2=20\) => \(BE=\sqrt{20}=2\sqrt{5}\)

b, Trong tam giác ACD có góc \(\widehat{C}=90^0\) nên ta có:

\(tan\widehat{DAC}= \dfrac{CD}{AC}=\dfrac{2}{4}=\dfrac{1}{2}\) => \(\widehat{DAC}\approx 26^034'\)

Vì \(\widehat{DAC}\) và \(\widehat{CDA}\) là hai góc phụ nhau trong một tam giác vuông ACD nên:

\(\widehat{CDA}\) = \(90^0\) - \(\widehat{DAC}\)  \(\approx 90^0-26^034'\approx 63^026'\)

Ta có hai tam giác ACD và tam giác ECB bằng nhau theo trường hơp cạnh - cạnh  - cạnh

=> \(\widehat{CDA}\) = \(\widehat{CBE}\approx 63^026'\)

Xét trong một tứ giác BCDX ta có:

\(\widehat{BXD}=360^0 - (\widehat{C}+\widehat{CDA}+\widehat{CBE})\) = \(360^0-(90^0 + 63^026'+ 63^026')\) = \(143^08'\)

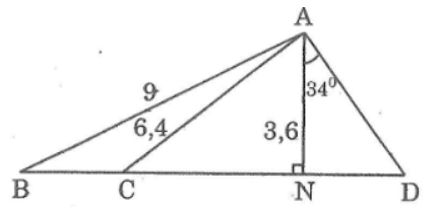
Bài 4: Cho một hình vẽ, biết rằng độ dài đoạn thẳng \(AB,AC,AN\) lần lượt là 9cm, 6,4cm và 3,6cm. Các góc \(\widehat{AND}\) và \(\widehat{DAN}\) có độ lớn lần lượt là \(90^0\) và \(34^0\). Hỏi:

a, Độ dài đoạn thẳng \(CN\) là bao nhiêu?

b, Độ lớn góc \(\widehat{ABN}\) và góc \(\widehat{CAN}\)

c,  Độ dài đoạn thẳng \(AD\) là bao nhiêu?

a, Trong tam giác ANC có góc \(\widehat{N}=90^0\),áp dụng định lý Py-ta-go ta có:

\(AC^2=AN^2+NC^2\) => \(NC^2=AC^2-AN^2\) = \(6,4^2-3,6^2= 28\)

=> \(NC=\sqrt{28}=2\sqrt{7}\)

b, Trong tam giác ANB có \(\widehat{N}=90^0\), áp dụng các công thức lượng giác trong tam giác vuông ta có:

\(sin\widehat{ABN}=\dfrac{AN}{AB}=\dfrac{3,6}{9}=0,4\) => \(\widehat{ABN}\approx 23^035'\)

Trong tam giác ANC có \(\widehat{N}=90^0\), áp dụng các công thức lượng giác trong tam giác vuông ta có:

\(cos\widehat{CAN}=\dfrac{AN}{AC}=\dfrac{3,6}{6,4}=\dfrac{9}{16}= 0,5625\) => \(\widehat{CAN}\approx 55^046'\)

d, Trong tam giác AND có \(\widehat{N}=90^0\), áp dụng các công thức lượng giác trong tam giác vuông ta có:

\(cos\widehat{NAD}=\dfrac{AN}{AD}\) => \(AD= \dfrac{AN}{cos\widehat{NAD}}\) => \(AD=\dfrac{3,6}{cos34^0}\) \(\approx 4,3424\)

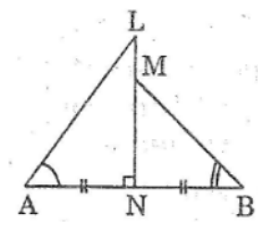
Bài 5: Cho hình vẽ. Biết rằng góc được tạo bởi hai đoạn thẳng là \(LN\) và \(AB\) có độ lớn là \(90^0\), giao nhau tại một điểm \(N\) (\(N\) thuộc \(AB\)). Một điểm \(M\) thuộc đoạn thẳng \(LN\). So sánh \(\widehat{LAN}\) và \(\widehat{MBN}\)

Trong tam giác ANL có \(\widehat{N}=90^0\), áp dụng các công thức lượng giác trong tam giác vuông ta có:

\(tan\widehat{LAN}=\dfrac{NL}{AN}\) (1)

Trong tam giác BMN có \(\widehat{N}=90^0\), áp dụng các công thức lượng giác trong tam giác vuông ta có:

\(tan\widehat{MBN}=\dfrac{NM}{BN}\) (2)

Theo dữ kiện đề bài ta lại có: \(AN=NB\) và \(NL>MN\) (3)

Vậy kết hợp cả ba biểu thức (1), (2) và (3) ta có thể rút ra \(tan\widehat{LAN}>tan\widehat{MBN}\)  

Vậy \(\widehat{LAN}>\widehat{MBN}\)

Bài 6: Biết rằng độ dài của các cạnh \(AB, AC, BC\) trong một tam giác ABC lần lượt là 3cm, 4cm, 5cm. Hãy tính các góc trong tam giác này?

Ta có \(AB^2+AC^2=3^2+4^2=9+16=25\) = \(BC^2\)

=> Vậy tam giác ABC là tam giác vuông tại \(\widehat{A}\) (áp dụng định lý Py-ta-go đảo)

Trong tam giác ABC có \(\widehat{A}=90^0\), áp dụng các công thức lượng giác trong tam giác vuông ta có:

\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}=0,8\) => \(\widehat{B}=53^08'\)

\(\widehat{C}=90^0-\widehat{B}=90^0-53^08'=36^052'\)

Tham khảo thêm >>> Giải bài tập sách giáo khoa bài 3 Toán 9 Bảng lượng giác

đã đem đến cho các bạn bài viết lý thuyết và các dạng bài tập tự luận về bảng lượng giác cơ bản và bảng lượng giác đặc biệt thông qua bài toán 9 bảng lượng giác. Nếu có thắc mắc hay đóng góp gì cho bài viết bảng lượng giác, các bạn hãy để lại comment dưới phần bình luận nhé!