Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 1 - Hình học 9

Đề bài

Bài 1. Không dùng bảng lượng giác và máy tính, hãy so sánh:

a. tan28˚ và sin28˚

b. tan32˚ và cos58˚

Bài 2. Cho ∆ABC vuông tại A. Chứng minh rằng:  \(\tan {{\widehat {ABC}} \over 2} = {{AC} \over {AB + BC}}\)

Hướng dẫn giải

Bài 1. a. Ta có: 0 0α>

\(\eqalign{  &  \Rightarrow \tan \alpha .\cos \alpha 

với \(α = 28^o\) , ta có: \(\sin28^o

Cách khác : Dựng ∆ABC vuông tại A và \(\widehat C = 28^\circ \)

Ta có: \(\sin 28^\circ  = {{AB} \over {BC}};\tan 28^\circ  = {{AB} \over {AC}}\)

mà \(BC > AC\) (cạnh huyền > cạnh góc vuông)

\( \Rightarrow {{AB} \over {BC}}

b. \(\cos 58^o = \sin(90^o - 58^o) = \sin 32^o\)

Theo chứng minh câu a : \(\sin32^o

Bài 2.

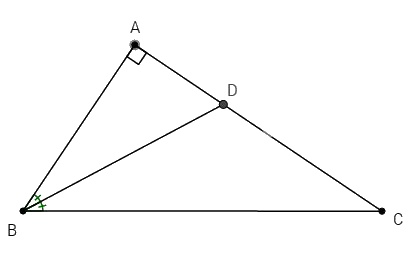
Vẽ phân giác BD, ta có: \({{DA} \over {DC}} = {{BA} \over {BC}}\)

\( \Rightarrow {{DA} \over {AB}} = {{DC} \over {BC}} = {{DA + DC} \over {AB + BC}} = {{AC} \over {AB + BC}}\) (1)

Mặt khác \(∆ABC\) vuông tại A, ta có:

\(\tan \widehat {ABD} = \tan {{\widehat {ABC}} \over 2} = {{DA} \over {AB}}\)

Từ (1) và (2) \( \Rightarrow \tan {{\widehat {ABC}} \over 2} = {{AC} \over {AB + BC}}\)

\tan32^o\)>{{ab}>\tan28^o\).p>\tan>