Bài C7 trang 123 SGK Vật lí 9
Tóm tắt bài
Đề bài
Vận dụng kiến thức hình học, tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh trong hai trường hợp ở C5 khi vật có chiều cao h = 6mm.
Hướng dẫn giải
Dựa vào tỷ số đồng dạng của hai tam giác đồng dạng
Lời giải chi tiết
Trường hợp 1- thấu kính hội tụ
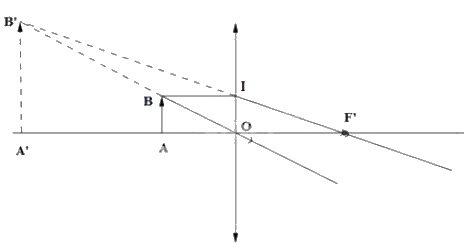
Tam giác BB'I đồng dạng với tam giác OB'F' cho ta:
\(\frac{BI}{OF}= \frac{BB'}{OB'}\) => \(\frac{8}{12}= \frac{BB'}{OB'}\) => \(\frac{12}{8}= \frac{OB'}{BB'}\) => \(\frac{BB' +OB}{BB'}\) = 1,5
1 + \(\frac{OB}{BB'}\) = 1,5 => \(\frac{OB}{BB'}\) = 0,5 = \(\frac{1}{2}\) => \(\frac{BB'}{OB}\) = 2
Tam giác OAB đồng dạng với tam giác OA'B', cho ta:
\(\frac{OA'}{OA}=\frac{A'B'}{AB}=\frac{OB'}{OB}\) (*)
Ta tính tỉ số: \(\frac{OB'}{OB}\) = \(\frac{OB + BB'}{OB}\) = 1 + \(\frac{BB'}{OB}\) = 1 + 2 = 3
Thay vào (*), ta có:
\(\frac{OA'}{OA}\) = 3 => OA' = 3. OA = 3.8 = 24 cm.
\(\frac{A'B'}{AB}\) = 3 => A'B' = 3. AB = 3. 6 = 18 mm.
Vậy ảnh có độ cao là 3cm, khoảng cách từ ảnh đến thấu kính là 24cm.
+ Với thấu kính phân kì:
Tam giác FB'O đồng dạng với tam giác IB'B, cho ta:
\(\frac{BI}{OF} =\frac{BB'}{OB'}\) = \(\frac{8}{12} =\frac{2}{3}\)
Tam giác OAB đồng dạng với tam giác OA'B', cho ta:
\(\frac{OA}{OA'} =\frac{OB}{OB'}=\frac{OB' + BB'}{OB'} = 1 + \frac{ BB'}{OB'} = 1 + \frac{2}{3} = \frac{5}{3}\)
\( \Rightarrow OA' = \frac{3}{5} OA = \frac{3}{5} .8 = 4,8 cm.\)
\(\frac{AB}{A'B'} = \frac{OB}{OB'}\) = \(\frac{OB' + BB'}{OB'}= 1 + \frac{ BB'}{OB'} = 1 + \frac{2}{3} = \frac{5}{3}\)
\( \Rightarrow {{AB} \over {A'B'}} = {5 \over 3}\)
\(\Rightarrow A'B' = {3 \over 5}AB = {3 \over 5}.6 = 3,6mm = 0,36cm\)
Vậy ảnh cao 0,36 cm và cách thấu kính 4,8 cm.
Copyright © 2021 HOCTAP247
