Giải câu 7 Trang 100 - Sách giáo khoa Vật lí 10

     Chọn C. 14 (N).

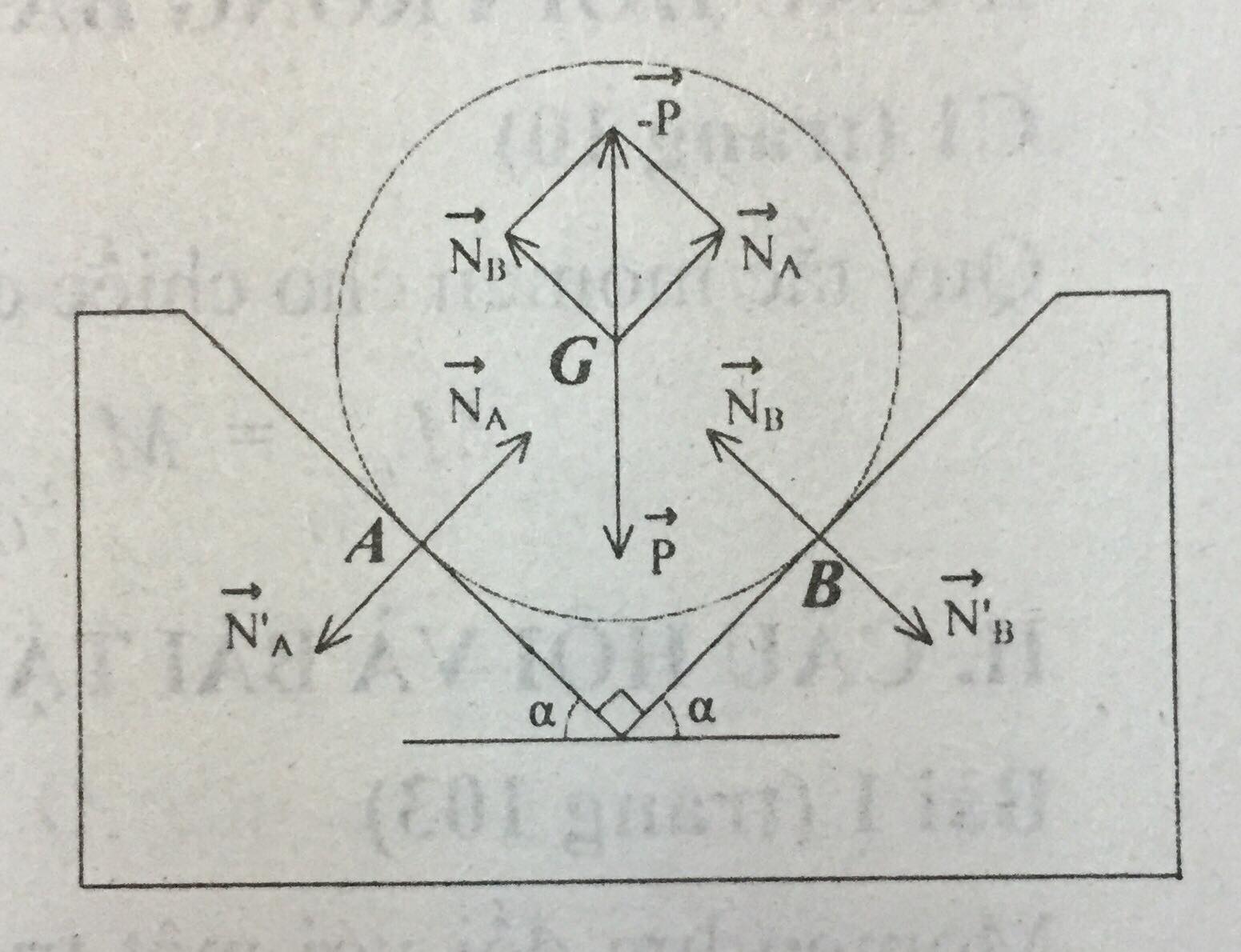
     Quả cầu cân bằng dưới tác dụng của ba lực đồng quy:

     - Trọng lượng \(\vec{P}\) đặt tại trọng tâm G của vật.

     - Phản lực của giá đỡ tại điểm A: \(\vec{N_A}\) có giá vuông góc với mặt tiếp xúc và đi qua G.

     - Phản lực của giá đỡ tại điểm B: \(\vec{N_B}\) có giá vuông góc với mặt tiếp xúc và đi qua G.

     Trượt \(\vec{N_A},\vec{N_B}\) đến G và áp dụng điều kiện cân bằng của vật ta có:

              \(\vec{N_A}+\vec{N_B}+\vec{P}=\vec{0}\)

     Suy ra  \(\vec{N_A}+\vec{N_B}=-\vec{P}\)

     Vì \(\vec{N_A}\) vuông góc với \(\vec{N_B}\) và \(\left | \vec{N_A} \right |=\left | \vec{N_B} \right |\) nên hình bình hành vectơ là hình vuông, ta có:

               \(N_A=N_B=\dfrac{P}{\sqrt{2}}=\dfrac{mg}{\sqrt{2}}=\dfrac{2.10}{\sqrt{2}}=10 \sqrt{2}(N)\)

     Theo định luật III Niu - tơn ta có:

     - Áp dụng của quả cầu lên giá đỡ trái: \(N'_A=N_A=10 \sqrt{2} \approx 14(N)\)

     - Áp dụng của quả cầu lên giá đỡ phải: \(N'_B=N_B=10 \sqrt{2} \approx 14(N)\).