Giải câu 5 Trang 106 - Sách giáo khoa Vật lí 10
Tóm tắt bài
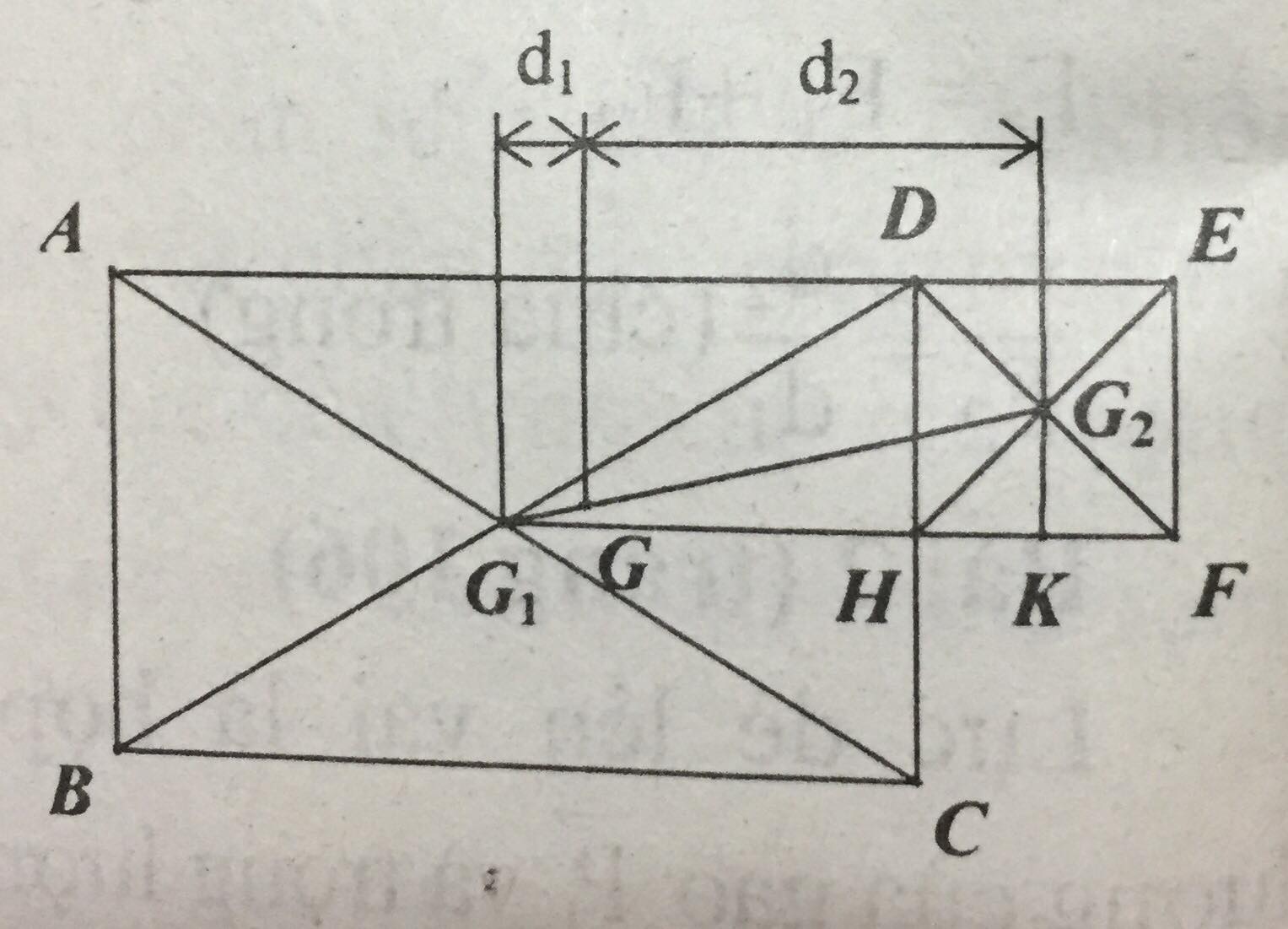
Bản phẳng được ghép bởi hai hình chữ nhật ABCD và DEFH.
Trọng lượng của bản phẳng là hợp của trọng lượng của hai hình chữ nhật.
Diện tích ABCD: \(S_1=6.9=54(cm^2)\)
Trọng lượng của ABCD:
\(P_1=m_1g=DS_1hg\) (1)
Trong đó, D là trọng lượng riêng của chất làm bản phẳng, h là bề dày của bản phẳng.
Diện tích DEFH: \(S_2=3.3=9(cm^2)\)
Trọng lượng của DEFH:
\(P_2=DS_2hg\) (2)
Từ (1) và (2) suy ra \(\dfrac{P_1}{P_2}=\dfrac{S_1}{S_2}=\dfrac{54}{9}=6\)
Theo định lí Ta - lét ta có: \(\dfrac{d_2}{d_1}=\dfrac{GG_2}{GG_1}\)
Theo định lí Pi - ta - go ta có:
\(G_1G_2=\sqrt{G_1K^2+G_2K^2}=\sqrt{6^2+1,5^2} \approx 6,18(cm)\)
Áp dụng quy tắc hợp lực song song ta được:
\(\dfrac{GG_2}{GG_1}=\dfrac{d_2}{d_1}=\dfrac{P_1}{P_2}=6 \Rightarrow GG_1=\dfrac{G_1G_2}{7}=\dfrac{6,18}{7} \approx 0,88(cm)\)
Copyright © 2021 HOCTAP247
