Bài 2 trang 176 SGK Đại số và Giải tích 11
Tóm tắt bài
Đề bài
Tính đạo hàm của các hàm số sau
a) \(y = 2\sqrt x {\mathop{\rm sinx}\nolimits} - {{\cos x} \over x}\)
b) \(y = {{3\cos x} \over {2x + 1}}\)
c) \(y = {{{t^2} + 2\cot t} \over {\sin t}}\)
d) \(y = {{2\cos \varphi - \sin \varphi } \over {3\sin \varphi + \cos \varphi }}\)
e) \(y = {{\tan x} \over {\sin x + 2}}\)
f) \(y = {{\cot x} \over {2\sqrt x - 1}}\)
Hướng dẫn giải
Sử dụng bảng đạo hàm cơ bản và các quy tắc tính đạo hàm của tích, thương.
Lời giải chi tiết
a)
\(y' =\left (2\sqrt x {\mathop{\rm sinx}\nolimits} - {{\cos x} \over x}\right)'\)
\(\eqalign{
& = 2{1 \over {2\sqrt x }}\sin x + 2\sqrt x\cos x - {{ - x\sin x - \cos x} \over {{x^2}}} \cr
& = {{x\sqrt x \sin x + 2{x^2}\sqrt x\cos x + x\sin x + \cos x} \over {{x^2}}} \cr
& = {{x(\sqrt x + 1)\sin x + (2{x^2}\sqrt x + 1)cosx} \over {{x^2}}} \cr} \)
\(\begin{array}{l}
b)\,\,y' = \dfrac{{ - 3\sin x\left( {2x + 1} \right) - 2.3\cos x}}{{{{\left( {2x + 1} \right)}^2}}}\\
\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 6x\sin x - 3\sin x - 6\cos x}}{{{{\left( {2x + 1} \right)}^2}}}
\end{array}\)
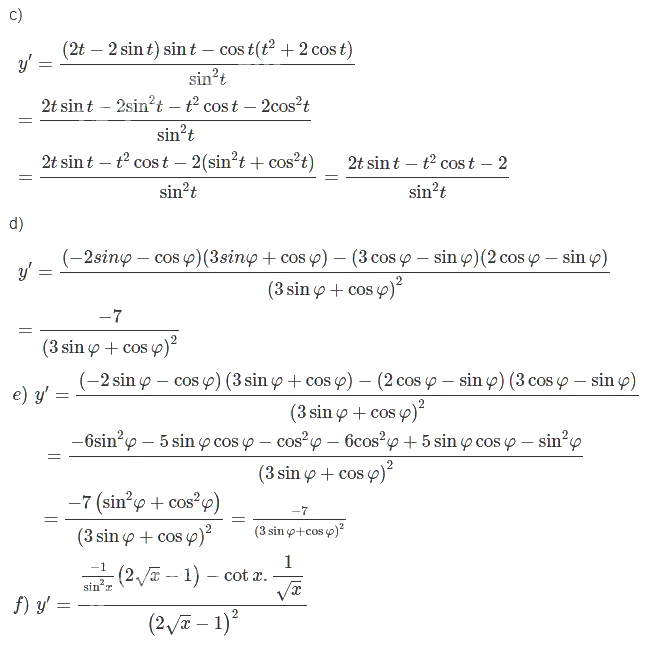
Copyright © 2021 HOCTAP247
