Những lí thuyết cần nắm được về Phép tịnh tiến chuẩn nhất - Toán 11

Bài viết này sẽ bao gồm đầy đủ các kiến thức lí thuyết về phép tịnh tiến, mong rằng sau bài viết này bạn sẽ có thể trả lời được các câu hỏi như có bao nhiêu phép tịnh tiến biến hình vuông thành chính nó, hay có bao nhiêu phép tịnh tiến biến đường thẳng thành chính nó,... và làm được các bài tập phép tịnh tiến.

I) Tìm hiểu chung

1) Định nghĩa

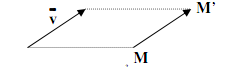
Trên một mặt phẳng, cho vecto \(\vec{v} = (a;b)\)

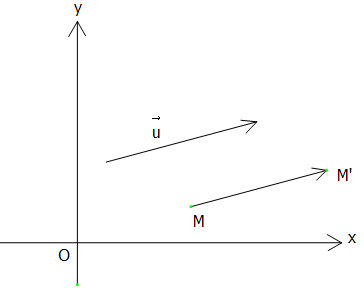
Phép tịnh tiến theo \(\vec{v} = (a;b)\) là phép biến hình, biến điểm M thành điểm M' sao cho \(\vec{MM'}=\vec {v}\).

2. Ký hiệu

\(T_{\vec{v}}(M))=M'\) hoặc \(T_{\vec{v}}:M\rightarrow M'\)

 

3. Tính chất

3.1) Tính chất 1:

Cho hai điểm M, N

Nếu phép tịnh tiến biến hai điểm trên thành hai điểm M',N' thì MN = M'N'

3.2) Tính chất 2: Gồm một định lý và một hệ quả

- Định lý: Cho ba điểm thẳng hàng M,N,P. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng mà không làm thay đổi thứ tự của ba điểm đó.

- Hệ quả:

+) Biến đường thẳng thành đường thẳng

+) Biến một tia thành một tia

+) Biến một đoạn thẳng thành một đoạn thẳng

+) Biến một tam giác thành một tam giác bằng nó

+) Biến một đường tròn thành một đường tròn bằng bán kính ban đầu

+) Biến góc thành góc bằng góc ban đầu.

4) Biểu thực tọa độ

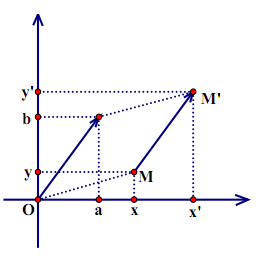
Cho vecto \(\vec{v} = (a;b)\) và điểm M (x;y)

Phép tịnh tiến sẽ biến điểm M thành điểm M'(x';y'), trong đó: \(\left\{\begin{matrix}x'=a+x & \\ y'=y+b & \end{matrix}\right.\)

(Hình ảnh minh họa)

 

II) Các dạng bài tập phép tịnh tiến

1. Dạng 1

Cho tọa độ của một điểm bất kì, yêu cầu tìm tọa độ của điểm ảnh qua phép tịnh tiến, cho vecto.

\(A(x;y)\); \(T_{\vec{v}}\) với \(\vec{v}=(x_0;y_0)\) \(\rightarrow A'(x';y')?\)

Phương pháp:

Áp dụng định lí 1 ta có:

  \(A'=T_{\vec{v}}(A) <=> \vec{AA'}=\vec{v} <=> (x'-x;y'-y)=(x_0;y_0) <=> \left\{\begin{matrix}x'-x=x_0 & \\ y'-y=y_0& \end{matrix}\right.<=> \left\{\begin{matrix}x'=x+ x_0 & \\ y'=y+ y_0 &\end{matrix}\right.\)

2. Dạng 2; 

Cho một đường thưởng, yêu cầu tìm ảnh của đường thẳng đó qua phép tịnh tiến với vecto đã cho.

\(d:ax+by+c=0\), \(T_{\vec{v}}\) với \(\vec{v}=(x_0;y_0)\)

Phương pháp:

Điểm M(x;y) thuộc d => \(T_{\vec{v}}(M)=M'(x';y') \in d'\)

Ta có biểu thức tọa độ \(T_{\vec{v}}\): \(\left\{\begin{matrix}x'=x+ x_0 & \\ y'=y+ y_0 &\end{matrix}\right.<=>\left\{\begin{matrix}x'-x=x_0 & \\ y'-y=y_0& \end{matrix}\right.\)

Suy ra \(d': a(x'-x_0)+b(y'-y_0)+c=0<=>ax'+by'-ax_0-by_0+c=0\)

Kết luận:\(d:ax+by-ax_0-by_0+c=0\)

Xem thêm >>> Hướng dẫn giải bài tập phép tịnh tiến lớp 11

Trên đây là bài viết tổng hợp lí thuyết cũng như phương pháp giải bài tập phép tịnh tiến và muốn gửi đến bạn. Chúc các bạn học tập tốt <3