Bài 2 trang 59 SGK Hình học 11

Đề bài

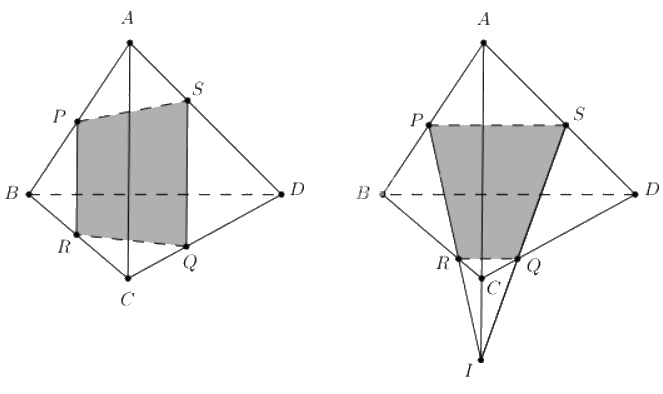
Cho tứ diện \(ABCD\) và ba điểm \(P, Q, R\) lần lượt trên ba cạnh \(AB, CD, BC\). Tìm giao điểm \(S\) của \(AD\) và mặt phẳng \((PQR)\) trong hai trường hợp sau đây.

a) \(PR\) song song với \(AC\)

b) \(PR\) cắt \(AC\)

Hướng dẫn giải

Sử dụng định lí 2 (về giao tuyến của ba mặt phẳng):

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

Lời giải chi tiết

a) Nếu \(PR // CA\) thì \(( PRQ) ∩ (ACD) = QS // CA // PR ( S ∈ AD)\).

b) Nếu \(PR ∩ AC = I\) thì trong \((ACD)\) kéo dài \(IQ\) cắt \(AD\) tại \(S\).