Chuyên đề sự đồng biến nghịch của hàm số lớp 12
Tóm tắt bài
Chuyên đề sự đồng biến nghịch của hàm số lớp 12
Bài viết hôm nay xin giới thiệu với các bạn về cách làm bài sự đồng biến nghịch biến của hàm số!
I. Xét sự đồng biến nghịch biến của hàm số
Kí hiệu K là một khoảng, một nửa hoặc 1 đoạn như sau:
- Hàm số f(x) đồng biến trên tập K, nếu mỗi cặp \(x_1,x_2\in K\) mà \(f(x_1)>f(x_2)\).
- Hàm số f(x) nghịch biến trên tập K, nếu mỗi cặp \(x_1,x_2\in K\) mà \(f(x_1)< f(x_2)\).
II. Các định lý
Cho hàm số y = f(x) xác định trên K và có đạo hàm thuộc tập xác định. Ta có các định lý sau đây:
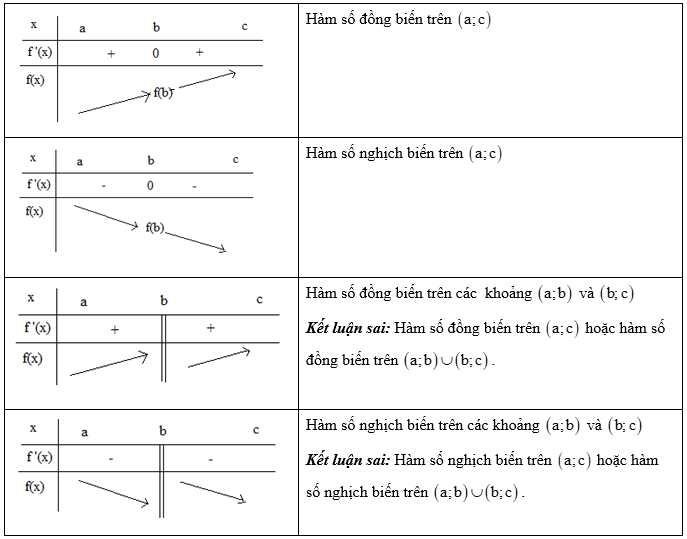
III. Bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số
Câu 1: Đồ thị hàm số \(y=\dfrac{3}{1-x}\) có tâm đối xứng là:
A. (3;1)
B. (1;3)
C. (1;0)
D. (0;1)
Câu 2: Cho hàm số sau \(y=x^3-3x^2+3\) có tập xác định là đoạn [1;3]. Tìm tổng M và m biết hai giá trị đó lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số ban đầu:
A. 8
B. 4
C. 2
D. 6
Câu 3: Cho hàm số \(y=\dfrac{x-1}{x+2}\) có đồ thị H. Tiếp tuyến của H tại giao điểm của H với trục Ox có phương trình là:
A. y=3x
B. y=3x-3
C. y=x-3
D. y= x+2
Câu 4: Cho hàm số \(y=\dfrac{2x+3}{x+2}\) có đồ thị C và đường thằng d=x+m. Với giá trị nào của m thì d cắt C tại 2 điểm phân biệt?
A. m<2
B. m>6
C. 2
D. m<2 hoặc m>6
Câu 5: Giá trị cực đại của hàm số \(y=x^3-3x^2-3x+2\) là:
A. \(-3+4\sqrt{2}\)
B. \(-3-4\sqrt{2}\)
C. \(3+4\sqrt{2}\)
D. \(-3-4\sqrt{2}\)
Trên đây là toàn bộ kiến thức mà muốn chia sẻ về các dạng bài tập sự đồng biến nghịch biến của hàm số!
Copyright © 2021 HOCTAP247
