Lý thuyết về lực Lorenxơ

Lý thuyết về lực Lorenxơ

Bài viết dưới đây  sẽ giúp các bạn làm sáng tỏ nội dung lý thuyết về lực Lorenxơ!

I. Lý thuyết?

1. Định nghĩa

Trong vật lý học và điện từ học, lực Lorenxơ là lực tổng hợp của lực điện và lực từ tác dụng lên một điện tích điểm nằm trong trường điện từ.

Đơn vị của lực Lorenxơ: N - Newton

2. Công thức

Định luật phát biểu rằng nếu hạt có điện tích q (C) chuyển động với vận tốc v (m/s) trong điện trường E (V/m) và từ trường B (G) thì nó sẽ chịu lực tác dụng lên nó. Định luật 3 Newton phát biểu về lực và phản lực, do vậy mặc dù phản lực của từ trường là nhỏ nhưng nó phải được tính đến. Lực Lorentz bằng:

\({\displaystyle \mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}\)

Các công thức phát sinh từ công thức cơ bản này miêu tả lực từ tác dụng lên dây dẫn có dòng điện chạy qua (đôi khi gọi là lực Laplace), phương của lực Lorenxơ là lực điện từ trong một vòng dây di chuyển qua từ trường (một khía cạnh của định luật cảm ứng điện từ Faraday), và lực tác dụng lên điện tích điểm chuyển động với vận tốc gần bằng tốc độ ánh sáng (dạng tương đối tính của lực Lorentz).

Oliver Heaviside là người đầu tiên suy luận ra công thức cho lực Lorentz vào năm 1889, mặc dù một số nhà lịch sử cho rằng James Clerk Maxwell đã đưa ra nó trong một bài báo năm 1865.[2] Định luật được đặt theo tên của Hendrik Lorentz, người tìm ra công thức sau Heaviside một vài năm và ông đã nghiên cứu và giải thích chi tiết ý nghĩa của lực này.

3. Lực từ động

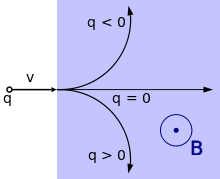
Thành phần gây ra bởi từ trường của lực này, còn gọi là lực từ hay đôi khi là lực Lorentz, có phương luôn vuông góc với phương chuyển động của hạt mang điện và làm thay đổi quỹ đạo chuyển động của hạt mang điện. Nếu hạt mang điện chuyển động theo phương vuông góc với đường cảm ứng từ thì hạt sẽ chuyển động theo quỹ đạo tròn, nếu hạt chuyển động theo phương không vuông góc với đường cảm ứng từ thì quỹ đạo của nó sẽ là hình xoắn ốc.

Lực tác động của từ trường lên dòng điện có nguyên nhân là thành phần này của lực Lorentz.

Lực từ giữa các cực của nam châm, cũng là tổng hợp lực gây ra bởi từ trường của nam châm này lên các electron chuyển động quanh nguyên tử ở nam châm kia, về bản chất cũng là thành phần này của lực Lorenxơ:

\({\displaystyle \mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}\)

II. Bài tập lực Lorenxơ có lởi giải

Bài 1: Biết rằng nguồn lực tác động vào e có U = 2000 V, cảm ứng từ bắt đầu xảy ra trong dây dẫn tạo ra 1 \(B = 10^{-3} T\) theo phương vuông góc với đường sức từ của từ trường. Biết khối lượng và điện tích của electron là m và e mà \(\dfrac{m}{|e|}=5,6875.10^{-12}(kg/C)\). Tính:

a) Bán kính quỹ đạo của các phần tử e?

b) Chu kì quay của các phần tử e?

Hướng dẫn:

Công của electron khi được gia tốc bởi hiệu điện thế U: A = qU = |e|U

Theo định lý biến thiên động năng ta có: Wđ2 – Wđ1 = A

Vì bỏ qua vận tốc của electron khi mới bắt đầu được gia tốc bởi hiệu điện thế U nên Wđ1 = 0

Chu kì quay của electron:

\(T=\dfrac{2\pi}{w}=\dfrac{2\pi r}{v}=\dfrac{2\pi m}{eB}=3,75.10^{-8}(cm)\)

Bài 2: Tính lực L trong các trường hợp cho trước:

a) α = 0°        b) α = 30°        c) α = 90°

Hướng dẫn:

Độ lớn của lực Lorenxơ: \(fL = Bv|q|sinα\)

a) Khi \(α = 0 ⇒ fL = Bv|q|sin0 = 0\)

b) Khi \(α = 30° ⇒ fL = Bv|q|sin30° = 0,5Bv|q|\)

Thay số: \(x fL = 0,5.1,5.3.10^7.1,6.10^{-19} = 3,6.10^{-12} (N)\)

c) Khi \(α = 90° ⇒ fL = Bv|q|sin90° = Bv|q|\)

Thay số: \( fL = 1,5.3.10^7.1,6.10^{-19} = 7,2.10^{-12} (N)\)

Với những gì mà đã giúp các bạn khái quát nội dung về công thức lực Lorenxơ trên đây, hy vọng sẽ giúp các bạn đạt kết quả cao trong học tập!