Khi một đường thẳng a và đường tròn (O;R) có 2 điểm chung ta nói đường thẳng a và đường tròn (O;R) cắt nhau. Đường thẳng a gọi là cát tuyến của đường tròn (O;R).

Khi đó: Gọi H là hình chiếu vuông góc của O lên a thì OH là khoảng cách từ O đến a và OH

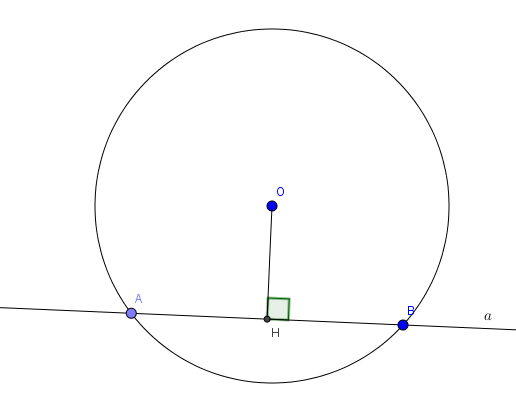
b) Đường thẳng và đường tròn tiếp xúc nhau

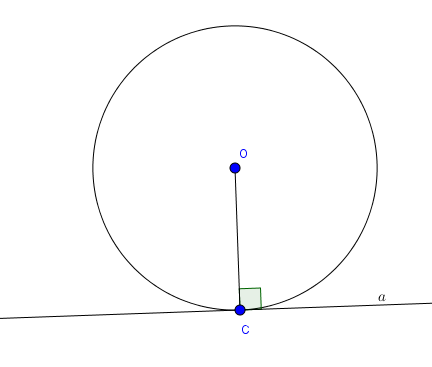
Khi đường thẳng a và đường tròn (O;R) có 1 điểm chung tại C ta nói đường thẳng a và đường tròn (O;R) tiếp xúc nhau.

Ta còn nói đường thẳng a là tiếp tuyến của đường tròn. Điểm C gọi là tiếp điểm và OC chính là khoảng cách từ O đến a. Khi đó OH=R

Định lý:

Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

c) Đường thẳng và đường tròn không giao nhau

Khi đường thẳng a và đường tròn (O) không có điểm chung nào thì ta nói đường thẳng a và đường tròn (O) không giao nhau

1.2. Hệ thức giữa khoảng cách từ tâm đường tròn tới đường thẳng và bán kính của đường tròn

Cho đường thẳng a và (O;R). Đặt OH=d là khoảng cách từ O đến đường thẳng a. Khi đó:

\(d
\(d=R\Leftrightarrow\) đường thẳng a có 1 điểm chung với (O;R) (hay đường thẳng a tiếp xúc với đường tròn (O;R))
\(d>R\Leftrightarrow\) đường thẳng a không có điểm chung với đường tròn (O;R)

2.1. Bài tập cơ bản

Bài 1: Cho tam giác ABC vuông tại A có AB=6, AC=8. Vẽ đường tròn (B;6). Hãy xác định vị trí tương đối của AC, BC với (B;6)

Hướng dẫn:

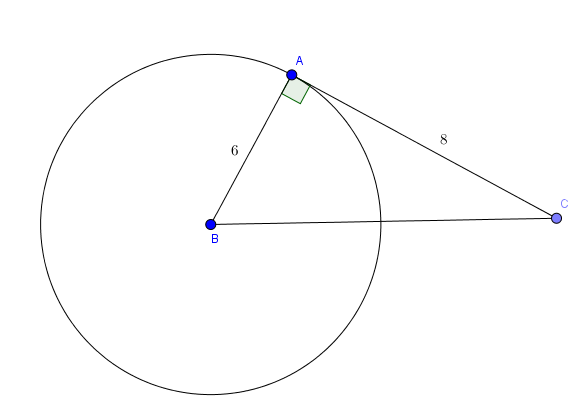
Vì \(BA\perp AC\) nên khoảng cách từ B đến AC chính bằng bán kính \(\Rightarrow\) AC tiếp xúc với (B;6)

BC đi qua B là tâm đường tròn nên khoảng cách từ B đến BC là 0 \(\Rightarrow\) BC cắt (B;6)

Bài 2: Trên mặt phẳng tọa độ Oxy cho A(5;3). Hãy xác định vị trí tương đối của (A;4) đối với các trục tọa độ

Hướng dẫn:

Khoảng cách từ A đến Oy chính là \(d=x_{A}=5\) và khoảng cách từ A đến Ox là \(d'=y_{A}=3\)

Vì d>4>d' nên (A;4) cắt Ox và không giao nhau với Oy

Bài 3: Cho đường tròn (O;10). M là một điểm cách O một khoảng 22. Gọi H là điểm bất kì trên đoạn OM, d=OH, đường thẳng xy vuông góc OM đi qua H

Tìm d để xy cắt, tiếp xúc và không giao với (O;10)

Hướng dẫn:

Để xy cắt (O;10) thì \(0\leq d<10\)

Để xy tiếp xúc với (O;10) thì \(d=10\)

Để xy không giao với (O;10) thì \(10

2.2. Bài tập nâng cao

Bài 1: Cho hình vuông ABCD. Trên đường chéo BD lấy H sao cho BH=BA, qua H vẽ đường thẳng vuông góc với BD cắt AD tại O.

a) So sánh OA; OH và HD

b) Xác định vị trí tương đối của BD với (O;OA)

Hướng dẫn:

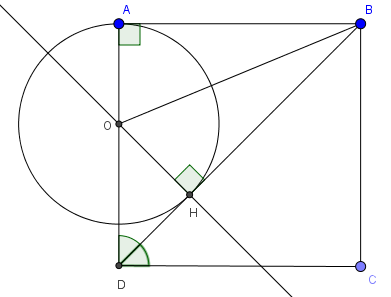
a) Xét tam giác OHD có \(\widehat{OHD}=90^{\circ};\widehat{ODH}=45^{\circ}\) nên tam giác OHD vuông cân. Vậy OH=HD

Xét 2 tam giác OAB và OHB có OB chung; \(\widehat{OAB}=\widehat{OHB}=90^{\circ}; BA=BH\Rightarrow \Delta OHB=\Delta OAB(ch-cgv)\)

\(\Rightarrow AO=OH\)

b) khoảng cách từ O đến BD chính là OH. mà OH=OA nên BD tiếp xúc với (O;OA)

Bài 2: Cho đường tròn (O;5), Từ điểm M ngoài (O) vẽ hai tiếp tuyến MA, MB sao cho \(MA\perp MB\) tại M

a) Tính MA, MB

b) Gọi I là giao điểm của OM với (O). Kẻ tiếp tuyến với (O) tại I và cắt OA, OB lần lượt ở C và D. Tính CD

Hướng dẫn:

a) Ta có: MA, MB là tiếp tuyến nên khoảng cách từ O đến MA và MB lần lượt là OA và OB ( do A,B là các giao điểm duy nhất với (O))

từ đó ta có: \(OA\perp MA, OB\perp MB\). Tứ giác OAMB có 3 góc vuông và OA=OB=R nên OAMB là hình vuông \(\Rightarrow MA=MB=R=5\)

b) Dễ dàng chứng minh được \(\Delta OAM=\Delta OBM\Rightarrow \widehat{BOM}=\widehat{AOM}=\frac{1}{2}\widehat{AOB}=45^{\circ}\)

Tam giác OID vuông tại I và có \(\widehat{IOD}=45^{\circ}\Rightarrow\) tam giác OID vuông cân và OI=ID. Tương tự: OI=IC

\(\Rightarrow CD=2.OI=2.R=10\)

3. Luyện tập Bài 4 Chương 2 Hình học 9

Qua bài giảng Vị trí tương đối của đường thẳng và đường tròn này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :

Ba vị trí tương đối của đường thẳng và đường tròn (cắt nhau, tiếp xúc, không giao nhau)
Hệ thức giữa khoảng cách từ tâm đường tròn tới đường thẳng và bán kính của đường tròn

3.1 Trắc nghiệm Vị trí tương đối của đường thẳng và đường tròn

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 4 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Câu nào trong các câu sau đây là câu đúng:
- A. Đường thẳng tiếp xúc với đường tròn khi đường thẳng đó có 2 giao điểm với đường tròn
- B. Đường thẳng cắt đường tròn khi đường thẳng đó có 1 giao điểm với đường tròn
- C. Đường thẳng không giao nhau với đường tròn khi nó chỉ có 1 giao điểm với đường tròn
- D. Đường thẳng cắt đường tròn khi đường thẳng đó có 2 giao điểm với đường tròn
Câu 2:
Cho điểm A(3;4). Khi đó đường tròn (A;R=4) sẽ có dạng như thế nào?
- A. Cắt Ox và tiếp xúc Oy
- B. Cắt Oy và tiếp xúc Ox
- C. Cắt cả Ox và Oy
- D. Tiếp xúc Ox và không giao Oy

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online

3.2 Bài tập SGK Vị trí tương đối của đường thẳng và đường tròn

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 4 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1

Bài tập 17 trang 109 SGK Toán 9 Tập 1

Bài tập 18 trang 110 SGK Toán 9 Tập 1

Bài tập 19 trang 110 SGK Toán 9 Tập 1

Bài tập 20 trang 110 SGK Toán 9 Tập 1