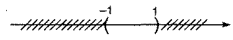Toán 10 Bài 4: Các tập hợp số
Tóm tắt bài
1.1. Các tập hợp số đã học
Tập hợp số tự nhiên: \(\mathbb{N} = \left\{ {0,1,2,3,4,...} \right\}.\)
\(\mathbb{N}*\) là tập hợp các số tự nhiên khác 0.
Tập hợp các số nguyên: \(\mathbb{Z} = \left\{ {..., - 2, - 1,0,1,2,...} \right\}.\)
Tập hợp các số hữu tỉ: \(Q = \left\{ {x = \frac{m}{n},m\,,n \in \mathbb{Z},n \ne 0} \right\}.\)
Tập hợp số thực: \(\mathbb{R}.\)
Ta có: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}.\)
Biểu đồ Ven các tập hợp số:
.jpg)
1.2. Các tập hợp con thường dùng của \({\mathbb{R}^{}}\)
a) Khoảng:
\((a;b) = \left\{ {x \in \mathbb{R}/a < x < b} \right\}\)
\(\left( {a; + \infty } \right) = \left\{ {x \in \mathbb{R}/x > a} \right\}\)
\(\left( { - \infty ;b} \right) = \left\{ {x \in \mathbb{R}/x < b} \right\}\)
b) Đoạn
\({\rm{[}}a;b{\rm{]}} = \left\{ {x \in \mathbb{R}/a \le x \le b} \right\}\)
c) Nửa khoảng
\(\left[ {a;b} \right) = \left\{ {x \in \mathbb{R}/a \le x < b} \right\}\)
\(\left( {a;b} \right] = \left\{ {x \in \mathbb{R}/a \le x < b} \right\}\)
\(\left[ {a; + \infty } \right) = \left\{ {x \in \mathbb{R}/x \ge a} \right\}\)
\(\left( { - \infty ;b} \right] = \left\{ {x \in \mathbb{R}/x \le b} \right\}\)
d) Kí hiệu:
\( + \infty :\) Dương vô cực (Hoặc dương vô cùng).
\( - \infty :\) Âm vô cực (Hoặc âm vô cùng).
Tập \(\mathbb{R}\) có thể viết \(\mathbb{R} = \left( { - \infty ; + \infty } \right).\) Gọi là khoảng \(\left( { - \infty ; + \infty } \right).\)
Ví dụ 1:
Xác định các tập hợp sau và biểu diễn chúng trên trục số:
a) \(\left[ { - 3;1} \right) \cup \left( {0;4} \right];\)
b) \(\left( { - 2;15} \right) \cup \left( {3; + \infty } \right);\)
c) \(\left( {0;2} \right) \cup \left[ { - 1;1} \right);\)
d) \(\left( { - \infty ;1} \right) \cup \left( { - 1; + \infty } \right);\)
e) \(\left[ { - 12;3} \right) \cap \left( { - 1;4} \right];\)
f) \(\left( {4;7} \right) \cap \left( { - 7; - 4} \right);\)
g) \(\left( {2;3} \right) \cap \left[ {3;5} \right);\)
h) \(\left( { - \infty ;1} \right) \cap \left( { - 1; + \infty } \right).\)
Hướng dẫn giải:
a) \(\left[ { - 3;1} \right) \cup \left( {0;4} \right] = \left[ { - 3;4} \right].\)
b) \(\left( { - 2;15} \right) \cup \left( {3; + \infty } \right) = ( - 2; + \infty ).\)
c) \(\left( {0;2} \right) \cup \left[ { - 1;1} \right) = {\rm{[}} - 1;2).\)
d) \(\left( { - \infty ;1} \right) \cup \left( { - 1; + \infty } \right) = ( - \infty ; + \infty ).\)
e) \(\left[ { - 12;3} \right) \cap \left( { - 1;4} \right] = {\rm{[}} - 1;3].\)
f) \(\left( {4;7} \right) \cap \left( { - 7; - 4} \right) = \emptyset .\)
g) \(\left( {2;3} \right) \cap \left[ {3;5} \right) = \emptyset .\)
h) \(\left( { - \infty ;1} \right) \cap \left( { - 1; + \infty } \right) = ( - 1;1).\)
Ví dụ 2:
Tìm m sao cho \(\left( {m - 7;m} \right) \subset \left( { - 4;3} \right).\)
Hướng dẫn giải:
\(\left( {m - 7;m} \right) \subset \left( { - 4;3} \right)\) khi và chỉ khi: \(\left\{ \begin{array}{l}m - 7 \ge - 4\\m \le 3\end{array} \right. \Leftrightarrow m = 3.\)
3. Luyện tập Bài 3 chương 1 đại số 10
Ở chương trình cấp 2, các em đã được học các tập hợp số tự nhiên, số nguyên, số hữu tỉ và số thực. Nội dung bài Các tập hợp số, không giới thiệu đếm các em những tập số mới mà sẽ giúp các em tìm hiểu các dạng tập con của tập số thực. Đây là bài học quan trọng, kiến thức được học sẽ được vận dụng lâu dài trong chương trình Toán phổ thông, đặc biệt là các bài toán liên quan đến bất phương trình.
3.1 Trắc nghiệm về các tập hợp số
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Chương 1 Bài 4 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. \(\left( {0;1} \right)\)
- B. \(\left[ {0;1} \right]\)
- C. \(\left[ { - 3;4} \right]\)
- D. \(\left[ { - 3;0} \right]\)
-
- A. \(\left( {0;1} \right)\)
- B. \(\left[ {0;1} \right)\)
- C. . \(\left( {0;1} \right]\)
- D. \(\left[ {0;1} \right]\)
-
- A. \(\left( { - 2;1} \right)\)
- B. \(\left( { - 2;1} \right]\)
- C. \(\left( { - 3; - 2} \right)\)
- D. \(\left( { - 2;5} \right)\)
-
- A. \(\left[ { - 4; - 2} \right]\)
- B. \(\left( {3;7} \right]\)
- C. \(\left[ { - 4; - 2} \right) \cup \left( {3;7} \right]\)
- D. \(\left[ { - 4;2} \right) \cap \left( {3;7} \right]\)
Câu 5- Câu 11: Xem thêm phần trắc nghiệm để làm thử Online
3.2 Bài tập SGK và Nâng Cao về các tập hợp số
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Chương 1 Bài 4 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
Bài tập 1 trang 18 SGK Đại số 10
Bài tập 2 trang 18 SGK Đại số 10
Bài tập 3 trang 18 SGK Đại số 10
Bài tập 1.31 trang 16 SBT Toán 10
Bài tập 1.32 trang 16 SBT Toán 10
Bài tập 1.33 trang 16 SBT Toán 10
Bài tập 1.34 trang 16 SBT Toán 10
Bài tập 1.35 trang 16 SGK Toán 10
Bài tập 1.36 trang 16 SGK Toán 10
4. Hỏi đáp về bài 4 chương 1 đại số 10
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.
Copyright © 2021 HOCTAP247

.PNG)
.PNG)
.PNG)
![Đoạn [a;b]](https://hoc247.net/fckeditorimg/upload/images/%5Ba%3Bb%5D.PNG)
.PNG)
![Nửa khoảng (a;b]](https://hoc247.net/fckeditorimg/upload/images/(a%3Bb%5D.PNG)
.PNG)
![Nửa khoảng (-vc;b]](https://hoc247.net/fckeditorimg/upload/images/(-vc%3Bb%5D.PNG)
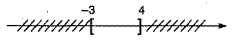
.PNG)