Vật lý 10 Bài 12: Lực đàn hồi của lò xo và Định luật Húc
Tóm tắt bài
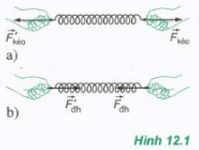
1.1. Hướng và điểm đặt của lực đàn hồi của lò xo
-
Lực đàn hồi xuất hiện ở 2 đầu của lò xo và tác dụng vào các vật tiếp xúc với lò xo, làm nó biến dạng
-
Hướng của lực đàn hồi ở mỗi đầu của lò xo ngược với hướng của ngoại lực gây biến dạng
-
Ví dụ: Hình 12.1 SGK
1.2. Độ cứng lực đàn hồi của lò xo.
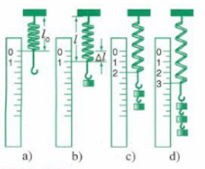
1.2.1. Thí nghiệm.
-
Treo quả cân có trọng lượng P vào lò xo thì lò xo giãn ra. Ở vị trí cân bằng ta có :
\(F = P = mg\)
-
Treo tiếp 1, 2 quả cân vào lò xo. Ở mỗi lần, ta chiều dài l của lò xo khi có tải rồi tính độ giãn \(\Delta l{\rm{ }} = l - {l_0}\)
-
Ta có kết quả :
1.2.2. Giới hạn đàn hồi của lò xo.
-
Mỗi lò xo hay mỗi vật đàn hồi có một giới hạn đàn hồi nhất định.
1.2.3. Định luật Húc (Hookes).
-
Trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.
\({F_{dh}} = {\rm{ }}k.|\Delta l|\)
k gọi là độ cứng (hay hệ số đàn hồi) của lò xo, có đơn vị là N/m.
-
Khi quả cân đứng yên: \({F_{dh}} = P = mg\)
⇒ \(k = \frac{{mg}}{{\Delta l}}\) (N/m)
1.2.4. Chú ý.
-
Đối với dây cao su hay dây thép, lực đàn hồi chỉ xuất hiện khi bị ngoại lực kéo dãn. Vì thế lực đàn hồi trong trường hợp này gọi là lực căng.
-
Đối với mặt tiếp xúc bị biến dạn khi bị ép vào nhau thì lực đàn hồi có phương vuông góc với mặt tiếp xúc
Bài 1:
Phải treo một vật có trọng lượng bằng bao nhiêu vào một lò xo có độ cứng k = 100N/m để nó dãn ra được 10 cm?
Hướng dẫn giải:
Áp dụng công thức
\(\small F_{dh }= k|\Delta l|\)
⇒ \(F = 100.{\rm{ }}10.{\rm{ }}{10^{ - 2}} = 10{\rm{ }}N\)
Bài 2:
Một lò xo có chiều dài tự nhiên 30cm, khi bị nén lò xo dài 24cm và lực đàn hồi của nó bằng 5N. Hỏi khi lực đàn hồi của lò xo bị nén bắng10 N thì chiều dài của lò xo là bao nhiêu
Hướng dẫn giải:
-
Áp dụng công thức: F = k|∆l|
-
Khi lực đàn hồi là 5N:
\({F_{dh}} = k|\Delta {l_1}\left| = \right|{l_1}-{l_0}\left| { = k} \right|24-30|\)
-
Khi lực đàn hồi bằng 10N:
\[{F_{dh}} = k|\Delta {l_2}\left| = \right|{l_2}-{l_0}\left| { = k} \right|{l_2}-30|\]
-
Lấy
=
= 2
\(\small \Rightarrow l_2 - 30 = -12\) (do lò xo bị nén)
\(\small \Rightarrow l_2 = 30 -12 = 18cm\)
3. Luyện tập Bài 12 Vật lý 10
Qua bài giảng Lực đàn hồi của lò xo .Định luật Húc này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
-
Nêu được ví dụ về lực đàn hồi và những đặc điểm của lực đàn hồi của lò xo (điểm đặt, hướng).
-
Phát biểu được định luật Húc và viết hệ thức của định luật này đối với độ biến dạng của lò xo.
-
Vận dụng được định luật Húc để giải các bài tập trong bài.
3.1. Trắc nghiệm
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lý 10 Bài 12 cực hay có đáp án và lời giải chi tiết.
-
- A. 10N
- B. 20N
- C. 30N
- D. 40N
-
- A. 12cm
- B. 14cm
- C. 16cm
- D. 18cm
-
- A. 30N/m
- B. 25N/m
- C. 1,5 N/m
- D. 150N/m
-
- A. 18N
- B. 24N
- C. 16N
- D. 6N
Câu 5- Câu 11: Xem thêm phần trắc nghiệm để làm thử Online
3.2. Bài tập SGK và Nâng cao
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lý 10 Bài 12 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 4 trang 88 SGK Vật lý 10 nâng cao
Bài tập 12.1 trang 30 SBT Vật lý 10
Bài tập 12.2 trang 30 SBT Vật lý 10
Bài tập 12.3 trang 30 SBT Vật lý 10
Bài tập 12.4 trang 31 SBT Vật lý 10
Bài tập 12.5 trang 31 SBT Vật lý 10
Bài tập 12.6 trang 31 SBT Vật lý 10
Bài tập 12.7 trang 31 SBT Vật lý 10
Bài tập 12.8 trang 31 SBT Vật lý 10
Bài tập 12.9 trang 31 SBT Vật lý 10
Bài tập 12.10 trang 31 SBT Vật lý 10
Bài tập 12.11 trang 32 SBT Vật lý 10
4. Hỏi đáp Bài 12 Chương 2 Vật lý 10
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
Copyright © 2021 HOCTAP247

.PNG)