Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2022 môn Vật Lý Trường THPT Quang Trung
Cho mạch điện xoay chiều như hình vẽ. Điện dung...
Cho mạch điện xoay chiều như hình vẽ. Điện dung \(C\) có giá trị thay đổi được và cuộn dây thuần cảm. Điều chỉnh giá trị của \(C\) thì thấy: ở cùng thời điểm, số chỉ của \({{V}_{1}...
Câu hỏi :
Cho mạch điện xoay chiều như hình vẽ. Điện dung \(C\) có giá trị thay đổi được và cuộn dây thuần cảm. Điều chỉnh giá trị của \(C\) thì thấy: ở cùng thời điểm, số chỉ của \({{V}_{1}}\) cực đại thì số chỉ của \({{V}_{1}}\) gấp đôi số chỉ của \({{V}_{2}}\). Hỏi khi số chỉ của \({{V}_{2}}\) cực đại thì số chỉ của \({{V}_{2}}\) gấp bao nhiêu lần số chỉ \({{V}_{1}}\)?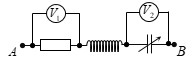
A. 2,5 lần
B. \(2\sqrt{2}\) lần
C. 2 lần
D. 1,5 lần
* Đáp án
A
* Hướng dẫn giải
+ Khi \(C\) thay đổi \({{V}_{1}}={{U}_{Rmax}}\) thì mạch xảy ra cộng hưởng, ta có
\({{V}_{1}}=2{{V}_{2}}\) ↔ \(R=2{{Z}_{L}}=2{{Z}_{C}}\), để đơn giản ta chọn \({{Z}_{L}}=1\) →\(R=2\).
+ Khi \({{V}_{2}}={{U}_{Cmax}}\), ta có \({{Z}_{{{C}'}}}=\frac{{{R}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}=\frac{{{2}^{2}}+{{1}^{2}}}{1}=5\)
→ \(\frac{{{V}_{2}}}{{{V}_{1}}}=\frac{\frac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}}{\frac{R}{\sqrt{{{R}^{2}}+\left( {{Z}_{L}}-Z_{C}^{2} \right)}}}=\frac{\frac{\sqrt{{{2}^{2}}+{{1}^{2}}}}{2}}{\frac{2}{\sqrt{{{2}^{2}}+{{\left( 1-5 \right)}^{2}}}}}=2,5\)→ Đáp án A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2022 môn Vật Lý Trường THPT Quang Trung
Số câu hỏi: 39
Copyright © 2021 HOCTAP247
