Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau \(20 \mathrm{~cm}\), dao động theo phương thẳng đứng với phương trình \(\mathrm{u}_{\mathrm{A}}=2 \cos (40...

* Hướng dẫn giải

Đáp án C

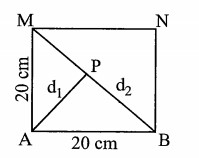
Bước sóng \(\lambda=1,5 \mathrm{~cm} .\)

Điều kiện để một điểm \(\mathrm{P}\) bất kì có biên độ cực đại với hai nguồn ngược pha: \(\mathrm{d}_{2}-\mathrm{d}_{1}=\left(\mathrm{n}+\frac{1}{2}\right) \lambda=1,5 \mathrm{n}+0,75\)

Điểm \(P\in \) đoạn MB nên \(\Delta {{\text{d}}_{\text{B}}}<\Delta {{\text{d}}_{P}}\le \Delta {{\text{d}}_{M}}\)

\(\Rightarrow 0-20<1,5 n+0,75 \leq 20 \sqrt{2}-20 \Rightarrow-13,8<n \leq 5,02\)

→ Có 19 giá trị n nguyên → Có 19 giá trị cực đại trên đoạn \(\mathrm{BM}\).