Hai thanh ray xA và yB đặt song song, cách nhau 20 cm trên mặt phẳng ngang. Lò xo có độ cứng k = 15 N/m liên kết với một thanh dẫn MN có khối lượng m = 200 g, có thể chuyển động tị...
Câu hỏi :
Hai thanh ray xA và yB đặt song song, cách nhau 20 cm trên mặt phẳng ngang. Lò xo có độ cứng k = 15 N/m liên kết với một thanh dẫn MN có khối lượng m = 200 g, có thể chuyển động tịnh tiến, không ma sát, luôn vuông góc và tiếp xúc với hai thanh ray. Hệ thống được đặt trong từ trường đều có phương vuông góc với mặt phẳng hình vẽ, có độ lớn B = 50 T. Tụ điện có điện dung C = 250 µF. Bỏ qua điện trở của hai thanh ray. Kích thích cho thanh MN dao động điều hòa với chu kỳ T. Giá trị của T gần giá trị nào nhất sau đây? 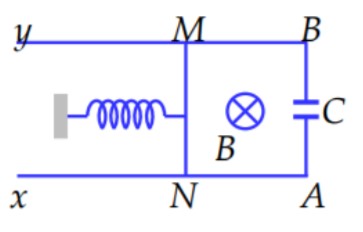
A. 0,657 s
B. 0,769 s
C. 1,336 s
D. 0,824 s.
* Đáp án
A
* Hướng dẫn giải
Thanh dẫn MN chuyển động, suất điện động tự cảm trong thanh là: \({{\text{e}}_{\text{c}}}=\text{B}l\text{v}\)
Điện tích của tụ điện là: \(\text{q}=\text{C}.{{\text{e}}_{\text{c}}}=\text{C}.\text{Blv}\)
Cường độ dòng điện chạy qua thanh MN là: \(\text{i}=\text{{q}'}=(\text{CBlv}{)}'=\text{CBla}\)
Lực từ tác dụng lên thanh MN là: \({{\text{F}}_{\text{t}}}=\text{iBl}=\text{C}{{\text{B}}^{2}}{{l}^{2}}\text{a}\)
Áp dụng định luật II Niu-tơn, ta có:
\({{F}_{dh}}+{{F}_{t}}=ma\Rightarrow -kx+C{{B}^{2}}{{l}^{2}}a=ma\)
\(\Rightarrow ~a.~\left( m-C{{B}^{2}}{{l}^{2}} \right)+kx=0\Rightarrow {x}''+\frac{k}{m-C{{B}^{2}}{{l}^{2}}}x=0\)
→ Thanh MN dao động điều hòa với tần số góc \(\omega =\sqrt{\frac{k}{m-C{{B}^{2}}{{l}^{2}}}}\)
Chu kì dao động của thanh là:
\(T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m-C{{B}^{2}}{{l}^{2}}}{k}}=2\pi \sqrt{\frac{0,2-{{250.10}^{-6}}{{.50}^{2}}.0,{{2}^{2}}}{15}}\approx 0,679(s)\)
Chu kì T gần nhất với giá trị 0,657 s
Chọn A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2022 môn Vật Lý - Trường THPT Nguyễn Duy Hiệu
Copyright © 2021 HOCTAP247
