Trong thí nghiệm giao thoa sóng với hai nguồn kết hợp A, B trên mặt nước, dao động cùng pha. Xét hai điểm C, D thuộc đường thẳng Ay vuông góc với AB tại A, với CA = 9 cm, DA = 16 c...

* Hướng dẫn giải

Ta có hình vẽ: 

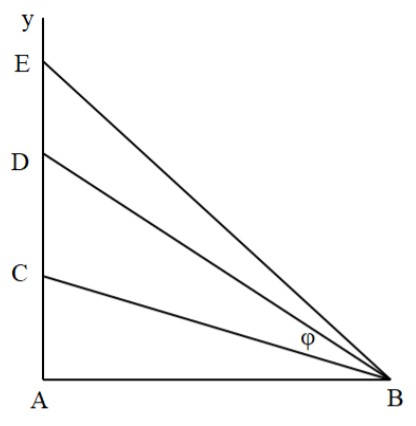
Để \(CB{{D}_{\max }}\Rightarrow {{\alpha }_{\max }}\Rightarrow {{(\tan \alpha )}_{\max }}\)

Xét \(\tan \alpha =\tan (ABD-ABC)=\frac{\tan ABD-\tan ABC}{1+\tan ABD\tan ABC}\)

\(\Rightarrow \tan \alpha =\frac{\frac{AD}{AB}-\frac{AC}{AB}}{1+\frac{AD}{AB}\cdot \frac{AC}{AB}}=\frac{AD-AC}{AB+\frac{AD.AC}{AB}}=\frac{7}{AB+\frac{144}{AB}}\)

Để \({{(\tan \alpha )}_{\max }}\Rightarrow {{\left( AB+\frac{144}{AB} \right)}_{\min }}\)

Áp dụng bất đẳng thức Cô – si, ta có: 

\(AB+\frac{144}{AB}\ge 2\sqrt{AB\cdot \frac{144}{AB}}\Rightarrow {{\left( AB+\frac{144}{AB} \right)}_{\min }}\Leftrightarrow AB=12(cm)\)

AB AB AB Tại C, D là hai cực đại liên tiếp

→ D là cực đại bậc k, C là cực đại bậc (k+1), ta có: 

\(\left\{ \begin{array}{*{35}{l}} DB-DA=\sqrt{D{{A}^{2}}+A{{B}^{2}}}-DA=k\lambda \Rightarrow k\lambda =4 \\ CB-CA=\sqrt{C{{A}^{2}}+A{{B}^{2}}}-CA=(k+1)\lambda \Rightarrow (k+1)\lambda =6 \\ \end{array}\Rightarrow \lambda =2(cm) \right.\)

Xét điểm E là cực tiểu xa A nhất → E là cực tiểu bậc 1 (k = 0) 

Ta có: 

\(EB-EA=\frac{1}{2}\lambda \Rightarrow \sqrt{E{{A}^{2}}+A{{B}^{2}}}-EA=\frac{1}{2}\lambda \)

\(\Rightarrow \sqrt{E{{A}^{2}}+{{12}^{2}}}-EA=1\Rightarrow EA=71,5(cm)\)

Chọn D.