Hai mô tô chuyển động thẳng đều khởi hành đồng thời ở 2 địa điểm cách nhau 18km. Nếu đi ngược chiều thì sau 12 phút hai xe gặp nhau. Nếu đi cùng chiều sau 11 giờ thì chúng đuổi kị...
Câu hỏi :
Hai mô tô chuyển động thẳng đều khởi hành đồng thời ở 2 địa điểm cách nhau 18km. Nếu đi ngược chiều thì sau 12 phút hai xe gặp nhau. Nếu đi cùng chiều sau 11 giờ thì chúng đuổi kịp nhau. Vận tốc của hai xe đó là:
A. 20km/h và 30km/h
B. 54km/h và 36km/h
C. 40km/h và 20km/h
D. 20km/h và 60km/h
* Đáp án
B
* Hướng dẫn giải
Gọi vận tốc của hai ô tô lần lượt là: v1,v2
Khoảng cách ban đầu giữa hai xe: s=18km
Ta có:
- Khi chuyển động ngược chiều:
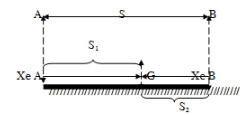
+ Do hai xe xuất phát đồng thời nên ta có thời gian chuyển động của hai xe cho đến khi gặp nhau: t=t1=t2=12ph=0,2h
+ Mặt khác, ta có:
\(\left\{ \begin{array}{l}
{t_1} = \frac{{{s_1}}}{{{v_1}}}\\
{t_2} = \frac{{{s_2}}}{{{v_2}}}
\end{array} \right. \to \left\{ \begin{array}{l}
{s_1} = {v_1}{t_1}\\
{s_2} = {v_2}{t_2}
\end{array} \right.\)
Lại có:
\(\begin{array}{*{20}{l}}
{{s_1} + {s_2} = s = 18km}\\
{ \leftrightarrow {v_1}.0,2 + {v_2}.0,2 = 18\left( 1 \right)}
\end{array}\)
- Khi chuyển động cùng chiều:
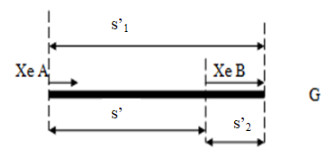
Ta có: \(s' = {s_1}^\prime - {s_2}^\prime = 20km\)
+ \({t_1}^\prime = {t_2}^\prime = t' = 1h\)
\(\left\{ \begin{array}{l}
{t_1}' = \frac{{{s_1}'}}{{{v_1}}}\\
{t_2}' = \frac{{{s_2}'}}{{{v_2}}}
\end{array} \right. \to \left\{ \begin{array}{l}
{s_1}' = {v_1}{t_1}'\\
{s_2}' = {v_2}{t_2}'
\end{array} \right.\)
Ta suy ra:
\(\begin{array}{*{20}{l}}
{{v_1}{t_1}^\prime - {v_2}{t_2}^\prime = 18}\\
{ \leftrightarrow {v_1} - {v_2} = 18\left( 2 \right)}
\end{array}\)
Từ (1),(2)(1),(2) ta suy ra:
\(\left\{ \begin{array}{l}
{v_1} = 54km/h\\
{v_2} = 36km/h
\end{array} \right.\)
Đáp án cần chọn là: B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi HK2 môn Vật Lý 8 năm 2021-2022 Trường THCS Hai Bà Trưng
Copyright © 2021 HOCTAP247
