Cho biểu thức f(x) = (x-3)(x+2)/(x^2-1). Hỏi có tất cả bao nhiêu giá trị nguyên âm của

* Hướng dẫn giải

Phương pháp giải:

+ Tìm TXĐ của \(f\left( x \right)\).

+ Giải bất phương trình \(f\left( x \right) < 1\).

Giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ { \pm 1} \right\}\)

Theo bài ra, ta có: \(f\left( x \right) < 1\)

\( \Leftrightarrow \frac{{\left( {x - 3} \right)\left( {x + 2} \right)}}{{{x^2} - 1}} < 1\)

\( \Leftrightarrow \frac{{\left( {x - 3} \right)\left( {x + 2} \right)}}{{{x^2} - 1}} - 1 < 0\)

\( \Leftrightarrow \frac{{{x^2} - x - 6 - {x^2} - 1}}{{{x^2} - 1}} < 0\)

\( \Leftrightarrow \frac{{ - x - 7}}{{{x^2} - 1}} < 0\)

Ta có bảng xét dấu:

$\Rightarrow x\in (-7;\mathrm{ }-1)\cup (1;\mathrm{ }+\mathrm{\infty })$

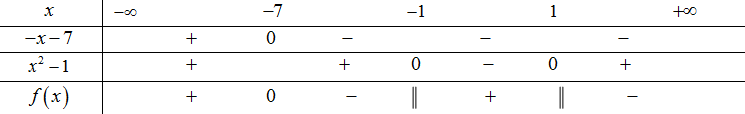
Mà \(x\) là số nguyên âm và $x\ne \mathrm{ }\pm 1$ nên $x\in \{-6;-5;\mathrm{ }-4;-3;\mathrm{ }-2\}$.

Vậy có 5 giá trị nguyên âm của \(x\) thỏa mãn điều kiện.