Trong không gian với hệ tọa độ Oxyz, cho hai điểm E(1;-2;4), F(1;-2;-3). Gọi M là điểm thuộc mặt phẳng

* Hướng dẫn giải

Phương pháp giải:

- Kiểm tra điểm \(E,{\mkern 1mu} F\) nằm khác phía so với mặt phẳng \[\left( {{\rm{Ox}}y} \right)\].

- \(ME + MF\) khi và chỉ khi M là giao điểm của EF và \[\left( {{\rm{Ox}}y} \right)\].

Giải chi tiết:

\(E\left( {1; - 2;4} \right),{\mkern 1mu} F\left( {1; - 2; - 3} \right)\) có $z_E=4>0,z_F=\mathrm{ }-3<0\Rightarrow E,F$ nằm khác phía so với mặt phẳng \[\left( {{\rm{Ox}}y} \right)\]

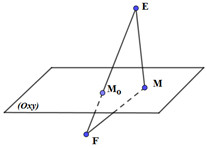
Khi đó, \(ME + MF \ge EF \Rightarrow {\left( {ME + MF} \right)_{\min }} = EF\) khi và chỉ khi \(M\) trùng với \[{M_0}\] là giao điểm của EF và  \[\left( {{\rm{Ox}}y} \right)\]

Ta có: $\overrightarrow{EF}\mathrm{ }=(0;0;-7)\Rightarrow EF:\left\{\begin{array}{l}x=1\\ y=-2\\ z=4-t\end{array}\right.\Rightarrow$Giả sử M0(1;−2;4−t)M0(1;−2;4−t)

Mà \[{M_0}\left( {1; - 2;4 - t} \right)\]

$M_0\in (Oxy)\Rightarrow 4-t=0\iff t=4\mathrm{ }\Rightarrow M_0(1;-2;0)$

Vậy, tổng \[ME + MF\] có giá trị nhỏ nhất khi và chỉ khi \[M\left( {1; - 2;0} \right)\].