Cho hình chóp (S.ABC) có SA vuông góc với mặt phẳng (ABC)

Xác định góc giữa hai mặt phẳng $(\alpha \mathrm{ }),(\beta \mathrm{ })$:

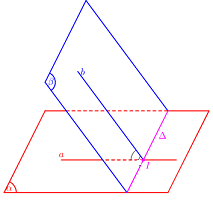
- Tìm giao tuyến \(\Delta \) của $(\alpha ),(\beta \mathrm{ })$.

- Xác định 1 mặt phẳng $(\gamma \mathrm{ })\perp \mathrm{\Delta }$.

- Tìm các giao tuyến $a=(\alpha )\cap \left(\gamma \mathrm{ }\right),b=(\beta \mathrm{ })\cap (\gamma )$

- Góc giữa hai mặt phẳng $(\alpha \mathrm{ }),(\beta \mathrm{ })$: $\left(\widehat{(\alpha \mathrm{ });(\beta \mathrm{ })}\right)=\left(\widehat{a;b}\right)$

Giải chi tiết:

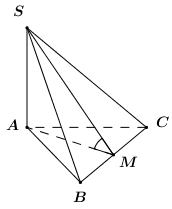
Gọi M là trung điểm của BC.

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AM \bot BC}\\{SA \bot BC}\end{array}} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM\).

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBC} \right) \cap \left( {ABC} \right) = BC}\\{SM \subset \left( {SBC} \right),{\mkern 1mu} SM \bot BC}\\{AM \subset \left( {ABC} \right),{\mkern 1mu} AM \bot BC}\end{array}} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SM;AM} \right) = \angle SMA\)

Tam giác SAM vuông tại A: \(SA = 1,{\mkern 1mu} {\mkern 1mu} AM = \frac{{2.\sqrt 3 }}{2} = \sqrt 3 \) (chiều cao của tam giác đều cạnh 2)

\( \Rightarrow \tan \angle SMA = \frac{{SA}}{{AM}} = \frac{1}{{\sqrt 3 }}\)

\( \Rightarrow \angle SMA = {30^0} \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = {30^0}\).