Số nguyên x lớn nhất để đa thức f(x) = (x+4)/(x^2-9) - 2/(x+3) - 4x/(3x-x^2) luôn âm

* Hướng dẫn giải

Phương pháp giải:

+ Tìm ĐKXĐ

+ \(f\left( x \right)\) luôn âm \( \Leftrightarrow f\left( x \right) < 0\). Từ đó giải bất phương trình và tìm được giá trị nguyên \(x\) lớn nhất.

Giải chi tiết:

ĐKXĐ: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 9 \ne 0}\\{x + 3 \ne 0}\\{3x - {x^2} \ne 0}\end{array}} \right.\)$\iff \{\begin{array}{c}x\ne \mathrm{ }\pm 3\\ x\ne 0\end{array}$

\(f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}}\) luôn âm \( \Leftrightarrow f\left( x \right) < 0\)

Ta có: \(f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}} < 0\)

\( \Leftrightarrow \frac{{x + 4}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} - \frac{2}{{\left( {x + 3} \right)}} + \frac{{4x}}{{x\left( {x - 3} \right)}} < 0\)

\( \Leftrightarrow \frac{{x\left( {x + 4} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} - \frac{{2x\left( {x - 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} + \frac{{4x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < 0\)

\( \Leftrightarrow \frac{{x\left( {x + 4} \right) - 2x\left( {x - 3} \right) + 4x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < 0\)

\( \Leftrightarrow \frac{{{x^2} + 4x - 2{x^2} + 6x + 4{x^2} + 12x}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < 0\)

\( \Leftrightarrow \frac{{3{x^2} + 22x}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < 0\)

\( \Leftrightarrow \frac{{x\left( {3x + 22} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < 0\)

\( \Leftrightarrow \frac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} < 0\)

$\Rightarrow x\in (-\mathrm{\infty };\mathrm{ }-\frac{22}{3})\cup (-3;3)$

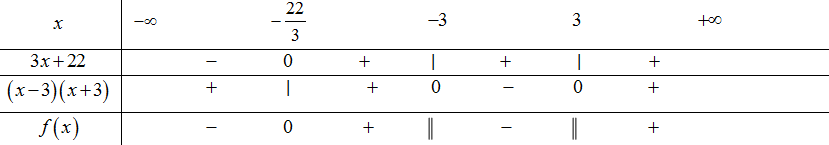
Vậy số nguyên \(x\) lớn nhất thỏa mãn đa thức luôn âm là \(x = 2\).