Có bao nhiêu số nguyên m để hàm số f(x) = x^4 - 2(m^2 - 3m)x^2 + 3 đồng biến

Phương pháp giải:

- Tính đạo hàm của hàm số.

- Chia các trường hợp của \(m\), xác định nghiệm của phương trình \(f'\left( x \right) = 0\).

- Lập BBT của hàm số, tìm điều kiện để \(f'\left( x \right) > 0{\mkern 1mu} {\mkern 1mu} \forall x \in \left( {2; + \infty } \right)\)

Giải chi tiết:

Ta có \(f'\left( x \right) = 4{x^3} - 4\left( {{m^2} - 3m} \right)x\).

\(f'\left( x \right) = 0 \Leftrightarrow 4x\left[ {{x^2} - \left( {{m^2} - 3m} \right)} \right] = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = {m^2} - 3m}\end{array}} \right.\)

TH1: \({m^2} - 3m \le 0 \Leftrightarrow 0 \le m \le 3\), khi đó ta có \(f'\left( x \right) > 0{\mkern 1mu} {\mkern 1mu} \forall x > 0\), do đó hàm số đồng biến trên \(\left( {0; + \infty } \right)\), thỏa mãn điều kiện hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\).

TH2: \({m^2} - 3m > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 3}\\{m < 0}\end{array}} \right.{\mkern 1mu} {\mkern 1mu} \left( * \right)\), khi đó ta có $f^{\text{'}}\left(x\right)=0\iff [\begin{array}{c}x=0\\ x=\sqrt{m^2-3m}=x_1\\ x=\mathrm{ }-\sqrt{m^2-3m}\mathrm{ }=x_2\end{array}$

Ta có BBT:

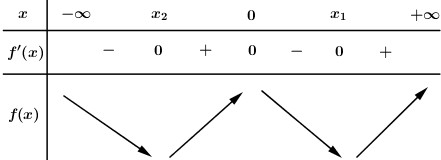
Dựa vào BBT ta thấy: Để hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\) thì \({x_1} \le 2\).

$\iff \sqrt{m^2-3m}\le 2\iff m^2-3m\le 4\iff -1\le m\le 4$.

Kết hợp điều kiện (*) \( \Rightarrow m \in \left[ { - 1;0} \right) \cup \left( {3;4} \right]\).

Kết hợp 2 trường hợp \( \Rightarrow m \in \left[ { - 1;4} \right]\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1;2;3;4} \right\}\).

Vậy có 6 giá trị của \(m\) thỏa mãn yêu cầu bài toán.