Biết rằng thiết diện qua trục của một hình nón là tam giác đều có diện tích bằng a^2 căn bậc hai của 3. Tính thể tích khối nón đã cho.

Phương pháp giải:

- Áp dụng công thức tính diện tích tam giác đều cạnh a: \(S = \frac{{{a^2}\sqrt 3 }}{4}\), từ đó suy ra độ dài đường sinh \(l\)và bán kính \(r\)của hình nón.

- Tính chiều cao của hình nón: \(h = \sqrt {{l^2} - {r^2}} \).

- Áp dụng công thức tính thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là: \(V = \frac{1}{3}\pi {r^2}h\).

Giải chi tiết:

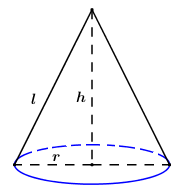
Vì thiết diện qua trục của hình nón là tam giác đều nên $l=2r$

\( \Rightarrow \) Bán kính hình nón là \(r = \frac{l}{2} = a\)và chiều cao hình nón là $h=\sqrt{l^2-r^2}\mathrm{ }=a\sqrt{3}.$

Vậy thể tích khối nón là $V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi a^2.a\sqrt{3}\mathrm{ }=\frac{\pi a^3\sqrt{3}}{3}.$