Một hình trụ (T) có hai đáy là hai hình tròn ( O;r ) và ( O';r ). Khoảng cách giữa hai đáy là

Phương pháp giải:

- Diện tích xung quanh của hình trụ có bán kính đáy là \(r\) và chiều cao của hình trụ bằng \(h\) là: \({S_{xq}} = 2\pi rh\).

- Diện tích xung quanh của hình nón có bán kính đáy bằng \(r\) và độ dài đường sinh bằng \(l\) là: \$(S_{xq}\mathrm{ }=\pi rl.$

Giải chi tiết:

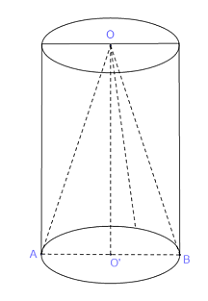
Gọi \(AB\) là đường kính đáy của hình tròn \(\left( {O,r} \right)\).

Hình trụ đã cho có độ dài bán kính đáy bằng \(r\) và độ dài đường cao là \(h = OO' = r\sqrt 3 \) nên diện tích xung quanh của hình trụ là: \({S_1} = 2\pi rh = 2\pi .r.\sqrt 3 r = 2\sqrt 3 \pi {r^2}\)

Hình nón có đáy là hình tròn \(\left( {O;r} \right)\) nên bán kính đáy của hình nón bằng \(r\). Độ dài đường sinh của hình nón là: $l=OA=\sqrt{O{O}^{\text{'}}+O{A}^2}\mathrm{ }=2a$

Suy ra diện tích xung quanh của hình nón là : \({S_2} = \pi rl = \pi r.2r = 2\pi {r^2}\).

Do đó tỉ số \(\frac{{{S_1}}}{{{S_2}}} = \frac{{2\sqrt 3 \pi {r^2}}}{{2\pi {r^2}}} = \sqrt 3 \).