Trang chủ
Đề thi & kiểm tra
Khác
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Cho hình hộp ABCD.A'B'C'D' (tham khảo hình vẽ). Gọi M...
Cho hình hộp ABCD.A'B'C'D' (tham khảo hình vẽ). Gọi M là trung điểm cạnh
Câu hỏi :
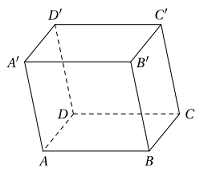
Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Gọi \(M\) là trung điểm cạnh \(A'D'\) và là mặt phẳng đi qua \(M\), song song với các đường thẳng \(BB',AC.\) Gọi \(T\) là giao điểm của đường thẳng \(BC\) và mặt phẳng . Tính tỉ số \(\frac{{TB}}{{TC}}.\)

A. 2
B \(\frac{2}{3}\)
C. 3
D. \(\frac{3}{2}\)
* Đáp án
* Hướng dẫn giải
Phương pháp giải:
+ Dựng mặt phẳng \(\left( \alpha \right)\) dựa vào mối quan hệ song song với \(BB',AC\)
+ Từ đó tính tỉ số \(\frac{{TB}}{{TC}}\)
Giải chi tiết:
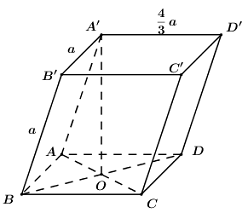
Gọi \(N,E\) lần lượt là trung điểm của \(AD,DC\)
Ta có \(MN//AA'//BB'\) và \(NE//AC\) (do \(NE\) là đường trung bình của tam giác \(DAC\))
Suy ra
Trong \(\left( {ABCD} \right)\), kéo dài \(NE\) cắt \(BC\) tại \(T\). Suy ra \(ANTC\) là hình bình hành (do \(AN//TC;NT//AC\))
Do đó \(TC = AN = \frac{1}{2}AD = \frac{1}{2}BC\)
Ta có \(\left( {MNE} \right) \cap BC = \left\{ T \right\}\) nên \(\frac{{TB}}{{TC}} = \frac{{\frac{3}{2}BC}}{{\frac{1}{2}BC}} = 3\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
