Trong không gian Oxyz, cho mặt cầu (S): (x-1)^2 + y^2 + (z-4)^2 = 9. Từ điểm

Phương pháp giải:

- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông.

Giải chi tiết:

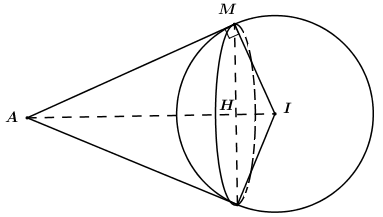
Mặt cầu (S) có tâm I(1;0;4), bán kính R = 3.

Gọi H là giao điểm của IA là mặt phẳng chứa đường tròn là tập hợp các điểm M. Khi đó H là tâm đường tròn tập hợp tiếp điểm, bán kính r = HM.

Ta có: $IA=\sqrt{3^2+0^2+{(-3)}^2}\mathrm{ }=3\sqrt{2}$.

Áp dụng định lí Pytago trong tam giác vuông IAM có: $AM=\sqrt{I{A}^2-I{M}^2}\mathrm{ }=\sqrt{18-9}\mathrm{ }=3$.

Áp dụng hệ thức lượng trong tam giác vuông IAM có: \(MH = \frac{{IM.AM}}{{IA}} = \frac{{3.3}}{{3\sqrt 2 }} = \frac{{3\sqrt 2 }}{2}\).