Trang chủ
Đề thi & kiểm tra
Khác
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Cho hàm số f(x)= ax^3+bx^2+cx+d (với a, b, c, d...
Cho hàm số f(x)= ax^3+bx^2+cx+d (với a, b, c, d thuộc R và a (a khác 0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số
Câu hỏi :
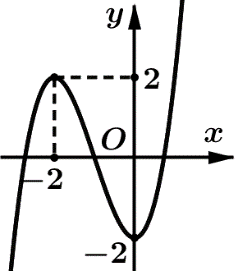
Cho hàm số (với \(b,\) \(c,\) và a \(a \ne 0\)) có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( { - 2{x^2} + 4x} \right)\) là

A. 2.
B. 5.
C. 4.
D. 3.
* Đáp án
* Hướng dẫn giải
Phương pháp giải:
- Tính đạo hàm của hàm số \(g\left( x \right)\)
- Giải phương trình \(g'\left( x \right) = 0\), xác định các nghiệm bội lẻ.
- Số nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\) là số điểm cực trị của hàm số.
Giải chi tiết:
Ta có: \(g'\left( x \right) = \left( { - 4x + 4} \right)f'\left( { - 2{x^2} + 4x} \right)\).
Cho , các nghiệm này đều là nghiệm đơn.
Do đó \(g'\left( x \right)\) đổi dấu tại đúng 5 điểm trên.
Vậy hàm số \(y = g\left( x \right)\) có 5 điểm cực trị.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
