Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên

Phương pháp giải:

Sử dụng công thức tính tỉ lệ thể tích: Cho các điểm \(M \in SA,N \in SB,P \in SC\) ta có: \(\frac{{{V_{SMNP}}}}{{{V_{SABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}}.\)

Giải chi tiết:

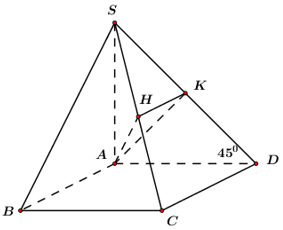
Ta có: \(\left( {SAB} \right) \cap \left( {SAD} \right) = \left\{ {SA} \right\}\)\( \Rightarrow SA \bot \left( {ABCD} \right).\)

\( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SD;{\mkern 1mu} {\mkern 1mu} AD} \right) = \angle SAD = {45^0}\)

\( \Rightarrow \Delta SAD\) là tam giác vuông cân tại \(A\)\( \Rightarrow h = SA = AD = a\).

Áp dụng công thức tỉ lệ thể tích ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{{V_{S.AHK}}}}{{{V_{S.ACD}}}} = \frac{{SA}}{{SA}}.\frac{{SH}}{{SC}}.\frac{{SK}}{{SD}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}.\)