Cho hàm số y = f(x), hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ.
Câu hỏi :
Cho hàm số , hàm số liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
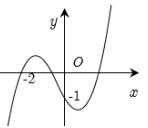
Bất phương trình \(f\left( x \right) < m - {x^3} - x\) (\(m\) là tham số thực) nghiệm đúng với mọi \(x \in \left( { - 2;0} \right)\) khi và chỉ khi:
Cho hàm số , hàm số liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

Bất phương trình \(f\left( x \right) < m - {x^3} - x\) (\(m\) là tham số thực) nghiệm đúng với mọi \(x \in \left( { - 2;0} \right)\) khi và chỉ khi:
* Đáp án
* Hướng dẫn giải
Phương pháp giải:
- Cô lập \(m\), đưa bất phương trình về dạng \(g\left( x \right) < m{\mkern 1mu} {\mkern 1mu} \forall x \in \left( { - 2;0} \right)\) \( \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 2;0} \right]} g\left( x \right)\).
- Lập BBT hàm số \(y = g\left( x \right)\) và kết luận.
Giải chi tiết:
Ta có: \(f\left( x \right) < m - {x^3} - x\)\( \Leftrightarrow f\left( x \right) + {x^3} + x < m{\mkern 1mu} {\mkern 1mu} \forall x \in \left( { - 2;0} \right)\).
Đặt \(g\left( x \right) = f\left( x \right) + {x^3} + x\) ta có \(g\left( x \right) < m{\mkern 1mu} {\mkern 1mu} \forall x \in \left( { - 2;0} \right)\)\( \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 2;0} \right]} g\left( x \right)\).
Ta có: \(g'\left( x \right) = f'\left( x \right) + 3{x^2} + 1\);
Số nghiệm của phương trình \(g'\left( x \right) = 0\) là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số
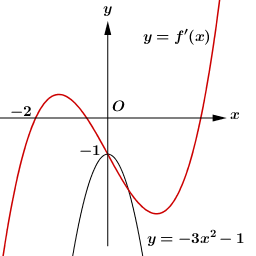
Dựa vào đồ thị hàm số ta thấy trên \(\left[ { - 2;0} \right]\), phương trình \(g'\left( x \right) = 0\) có duy nhất nghiệm \(x = 0\).
BBT hàm số \(y = g\left( x \right)\):
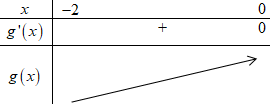
Dựa vào BBT ta thấy: \(\mathop {\max }\limits_{\left[ { - 2;0} \right]} g\left( x \right) = g\left( 0 \right) = f\left( 0 \right)\).
Vậy \(m \ge f\left( 0 \right)\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
