Cho hình lăng trụ (ABC.A'B'C') có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm

Phương pháp giải:

- Xác định đoạn vuông góc chung của hai đoạn thẳng \(AA'\) và BC.

- Áp dụng hệ thức lượng trong tam giác vuông tính \(A'G\).

- Áp dụng công thức tính thể tích \({V_{ABC.A'B'C'}} = A'G.{S_{ABC}}\).

Giải chi tiết:

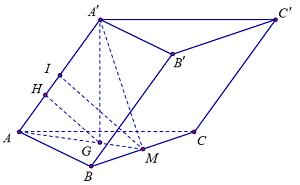
Gọi \(M\) là trung điểm của \(BC\). Vì tam giác \(ABC\) đều nên \(AM \bot BC\) và \(AM = \frac{{a\sqrt 3 }}{2}\)

\( \Rightarrow AG = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\).

Ta có \(A'G \bot \left( {ABC} \right)\) nên \(A'G \bot BC\); \(BC \bot AM\)\( \Rightarrow BC \bot \left( {MAA'} \right)\).

Trong \(\left( {AA'M} \right)\) kẻ \(MI \bot AA'\) tại \(I\); khi đó ta có \(BC \bot IM\) nên \(IM\) là đoạn vuông góc chung của \(AA'\) và \(BC\), do đó \(d\left( {AA';BC} \right) = IM = \frac{{a\sqrt 3 }}{4}.\)

Trong \(\left( {AA'M} \right)\) kẻ \(GH \bot AA'\) tại \(H\), áp dụng định lí Ta-lét ta có \(\frac{{AG}}{{AM}} = \frac{{GH}}{{IM}} = \frac{2}{3}\) \( \Leftrightarrow GH = \frac{2}{3}.\frac{{a\sqrt 3 }}{4} = \frac{{a\sqrt 3 }}{6}\)

Áp dụng hệ thức lượng trong tam giác vuông \(AA'G\)  ta có:

\(\frac{1}{{H{G^2}}} = \frac{1}{{A'{G^2}}} + \frac{1}{{A{G^2}}} \Leftrightarrow A'G = \frac{{AG.HG}}{{\sqrt {A{G^2} - H{G^2}} }} = \frac{{\frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 3 }}{6}}}{{\sqrt {\frac{{{a^2}}}{3} - \frac{{{a^2}}}{{12}}} }} = \frac{a}{3}\).

Tam giác \(ABC\) đều cạnh \(a\) nên \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\).

Vậy \({V_{ABC.A'B'C'}} = A'G.{S_{ABC}} = \frac{a}{3}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{{12}}\).