Trong không gian Oxyz, cho mặt cầu (S): x^2 + y^2 + z^2 + 2x - 4y - 2z + 9/2 = 0 và hai điểm A(0;2;0), B(2; - 6; - 2). Điểm

* Hướng dẫn giải

Phương pháp giải:

- Gọi \(E\) là trung điểm của \(AB\).

- Đánh giá GTNN của tích \(\overrightarrow {MA} .\overrightarrow {MB} \) đạt được dựa vào điểm \(E\).

Giải chi tiết:

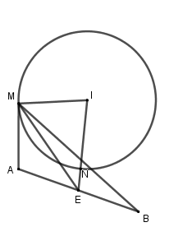
Mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;2;1} \right)\) và bán kính \(R = \frac{{\sqrt 6 }}{2}\).

Gọi \(E\) là trung điểm của \(AB\)\( \Rightarrow E\left( {1; - 2; - 1} \right)\) và \(AB = 6\sqrt 2 \).

Ta có: $\overrightarrow{MA}.\overrightarrow{MB}\mathrm{ }=(\overrightarrow{ME}\mathrm{ }+\overrightarrow{EA})(\overrightarrow{ME}\mathrm{ }+\overrightarrow{EB})$

$=M{E}^2+\overrightarrow{ME}.(\overrightarrow{EA}\mathrm{ }+\overrightarrow{EB})+\overrightarrow{EA}.\overrightarrow{EB}$

$=M{E}^2+\overrightarrow{ME}.\overrightarrow{0}-\overrightarrow{EB}.\overrightarrow{EB}\mathrm{ }=M{E}^2-\frac{1}{4}A{B}^2$

Suy ra \(\overrightarrow {MA} .\overrightarrow {MB} \) đạt GTNN khi \(ME\) đạt GTNN.

Lại có: \(ME + MI \ge IE \Rightarrow ME + MI \ge IN + NE \Rightarrow ME \ge NE\)

\( \Rightarrow ME\) đạt GTNN khi \(M \equiv N\) với \(N = IE \cap \left( S \right)\)

Đường thẳng \(IE\) đi qua \(I\left( { - 1;2;1} \right)\) và nhận $\overrightarrow{IE}\mathrm{ }=(2;-4;-2)$ làm VTCP nên $IE:\{\begin{array}{c}x=-1+t\\ y=2-2t\\ z=1-t\end{array}$

\(N = IE \cap \left( S \right)\) nên \({\left( { - 1 + t} \right)^2} + {\left( {2 - 2t} \right)^2} + {\left( {1 - t} \right)^2} + 2\left( { - 1 + t} \right) - 4\left( {2 - 2t} \right) - 2\left( {1 - t} \right) + \frac{9}{2} = 0\)

\( \Leftrightarrow 6{\left( {t - 1} \right)^2} + 12\left( {t - 1} \right) + \frac{9}{2} = 0\)

$\iff [\begin{array}{c}t-1=-\frac{1}{2}\\ t-1=\mathrm{ }-\frac{3}{2}\end{array}\iff [\begin{array}{c}t=\frac{1}{2}\\ t=-\frac{1}{2}\end{array}$\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{N\left( { - \frac{1}{2};1;\frac{1}{2}} \right) \Rightarrow NE = \frac{{3\sqrt 6 }}{2}}\\{N\left( { - \frac{3}{2};3;\frac{3}{2}} \right) \Rightarrow NE = \frac{{5\sqrt 6 }}{2}}\end{array}} \right.\)

\(M{E_{\min }} = \frac{{3\sqrt 6 }}{2}\) khi $M\equiv N(-\frac{1}{2};1;\frac{1}{2})\Rightarrow a+b+c=\mathrm{ }-\frac{1}{2}+1+\frac{1}{2}=1.$