Có bao nhiêu giá trị nguyên dương của tham số (m) để phương trình y = |x^3 - 3x + m| có 5 điểm cực trị

Phương pháp giải:

- Dựa vào số điểm cực trị để biện luận nghiệm của phương trình \(y = {x^3} - 3x + m\).

- Lập bảng biến thiên và suy ra các giá trị của \(m\).

Giải chi tiết:

Để phương trình \(y = \left| {{x^3} - 3x + m} \right|\) có 5 điểm cực trị thì phương trình \({x^3} - 3x + m = 0\) có 3 nghiệm phân biệt.

Ta có: \({x^3} - 3x + m = 0\)$\iff x^3-3x=-m.$

Đặt $f\left(x\right)=x^3-3x\Rightarrow f^{\text{'}}\left(x\right)=3x^2-3=0\iff x=\mathrm{ }\pm 1$

Bảng biến thiên:

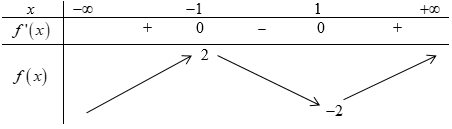
Dựa vào bảng biến thiên ta có $-2<-m<2\iff \mathrm{ }-2<m<2\Rightarrow m\in \{-1;0;1\}.$