Cho hình lăng trụ đứng (ABC.A'B'C') có đáy là tam giác cân tại A có AB = AC = 2a, góc CAB = 120^0. Mặt phẳng (AB'C') tạo với đáy một góc 60^0. Thể tích khối lăng trụ là:

Phương pháp giải:

- Xác định góc giữa hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {A'B'C'} \right)\) góc giữa hai mặt phẳng là góc giữa hai đường thẳng  nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường cao \(h = AA'\).

- Tính diện tích đáy \({S_{A'B'C'}}\), sử dụng công thức \(S = \frac{1}{2}ab\sin C\).

- Tính thể tích khối lăng trụ \(V = Sh\).

Giải chi tiết:

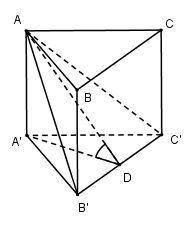
Gọi \(D\) là trung điểm của \(B'C'\). Vì tam giác \(A'B'C'\) cân tại \(A'\) nên \(A'D \bot B'C'\) (trung tuyến đồng thời là đường cao).

Ta có: \(\left. {\begin{array}{*{20}{l}}{A'D \bot B'C'}\\{AA' \bot B'C'}\end{array}} \right\} \Rightarrow B'C' \bot \left( {AA'D} \right) \Rightarrow B'C' \bot AD\)

\(\left\{ {\begin{array}{*{20}{l}}{\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'}\\{\left( {AB'C'} \right) \supset AD \bot B'C'}\\{\left( {A'B'C'} \right) \supset A'D \bot B'C'}\end{array}} \right.\)\( \Rightarrow \angle \left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right) = \angle \left( {AD;A'D} \right) = \angle ADA' = {60^0}\)

Vì tam giác \(A'B'C'\) cân tại \(A'\) nên \(\angle DA'C' = \frac{1}{2}\angle B'A'C' = {60^0}\)  (trung tuyến đồng thời là phân giác).

Xét tam giác vuông \(A'C'D\) có: \(A'D = A'C'.cos{60^0} = 2a.\frac{1}{2} = a.\)

Xét tam giác vuông \(AA'D\) có: \(AA' = A'D.\tan {60^0} = a.\sqrt 3 .\)

Ta có: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin \angle BAC = \frac{1}{2}.2a.2a.\frac{{\sqrt 3 }}{2} = {a^2}\sqrt 3 .\)

Vậy $V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=A{A}^{\text{'}}.S_{ABC}=a\sqrt{3}.a^2\sqrt{3}\mathrm{ }=3a^3.$