Xét các số thực dương x, y thỏa mãn log1/2x + log1/2y nhỏ hơn bằng log 1/2(x + y^2). Tìm giá trị nhỏ nhất

Đáp án: \({P_{\min }} = 9\)

Phương pháp giải:

+) Sử dụng công thức \({\log _a}x + {\log _a}y = {\log _a}\left( {xy} \right){\mkern 1mu} {\mkern 1mu} \left( {0 < a \ne 1,{\mkern 1mu} {\mkern 1mu} x,y > 0} \right)\), giải bất phương trình logarit cơ bản \({\log _a}f\left( x \right) \le {\log _a}g\left( x \right){\mkern 1mu} {\mkern 1mu} \left( {0 < a < 1} \right) \Leftrightarrow f\left( x \right) \ge g\left( x \right)\).

+) Rút \(x\) theo \(y\), thế vào \(P\).

+) Đưa \(P\) về dạng \(P = f\left( y \right)\). Lập BBT và tìm GTNN của \(P = f\left( y \right)\).

Giải chi tiết:

Theo bài ra ta có:

\[{\log _{\frac{1}{2}}}x + {\log _{\frac{1}{2}}}y \le {\log _{\frac{1}{2}}}\left( {x + {y^2}} \right) \Leftrightarrow {\log _{\frac{1}{2}}}\left( {xy} \right) \le {\log _{\frac{1}{2}}}\left( {x + {y^2}} \right) \Leftrightarrow xy \ge x + {y^2}\]

\[ \Leftrightarrow x\left( {y - 1} \right) \ge {y^2} > 0\]. Mà \[x > 0 \Rightarrow y - 1 > 0 \Leftrightarrow y > 1\].

\[ \Rightarrow x \ge \frac{{{y^2}}}{{y - 1}}\]. Khi đó ta có \(P = x + 3y \ge \frac{{{y^2}}}{{y - 1}} + 3y\) với \(y > 1\).

Xét hàm số \(f\left( y \right) = \frac{{{y^2}}}{{y - 1}} + 3y\) với \(y > 1\) ta có:

\(f'\left( y \right) = \frac{{2y\left( {y - 1} \right) - {y^2}}}{{{{\left( {y - 1} \right)}^2}}} + 3 = \frac{{{y^2} - 2y + 3{y^2} - 6y + 3}}{{{{\left( {y - 1} \right)}^2}}} = \frac{{4{y^2} - 8y + 3}}{{{{\left( {y - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = \frac{3}{2}}\\{y = \frac{1}{2}}\end{array}} \right.\)

BBT:

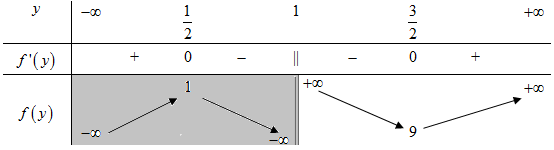
Từ BBT ta thấy \(\mathop {\min }\limits_{y > 1} f\left( y \right) = f\left( {\frac{3}{2}} \right) = 9\).

Vậy \(P \ge 9\) hay \({P_{\min }} = 9\).