Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là a, 2a, 3a có thể tích lớn nhất bằng

Đáp án: \({a^3}\)

Phương pháp giải:

Khối chóp có thể tích lớn nhất khi 3 cạnh đôi một vuông góc.

Giải chi tiết:

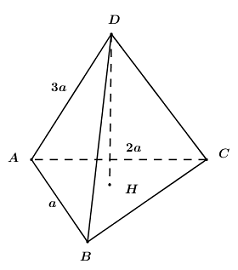
Giả sử khối chóp \(ABCD\) có \(AB = a,{\mkern 1mu} {\mkern 1mu} AC = 2a,{\mkern 1mu} {\mkern 1mu} AD = 3a\).

Gọi \(H\) là hình chiếu vuông góc của \(D\) lên \(\left( {ABC} \right)\), khi đó ta có: \(DH \bot \left( {ABC} \right)\) và \(DH \le AD\).

Ta có: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin \angle BAC \le \frac{1}{2}AB.AC\)

Vây \({V_{ABCD}} = \frac{1}{3}DH.{S_{\Delta ABC}} \le \frac{1}{3}AD.\frac{1}{2}AB.AC = \frac{1}{6}AB.AC.AD = \frac{1}{6}.a.2a.3a = {a^3}\)

Dấu “=” xảy ra \( \Leftrightarrow AD \bot \left( {ABC} \right),{\mkern 1mu} {\mkern 1mu} AB \bot AC\) hay \(AB,{\mkern 1mu} {\mkern 1mu} AC,{\mkern 1mu} {\mkern 1mu} AD\) đôi một vuông góc.