Cho hàm số y = f( x ), hàm số y = f'( x ) liên tục trên R có đồ thị như hình vẽ bên. Bất phương trình f(x) < 2x + m (m là tham số thực) nghiệm đúng với mọi
Câu hỏi :
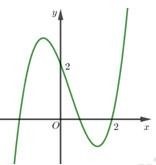
Cho hàm số \[y = f\left( x \right)\], hàm số \[y = f'\left( x \right)\] liên tục trên \[\mathbb{R}\] có đồ thị như hình vẽ bên. Bất phương trình \[f\left( x \right)\,\, < \,\,2x + m\] (m là tham số thực) nghiệm đúng với mọi \[x \in \left( {0;2} \right)\] khi và chỉ khi

A. \[m\,\, > \,\,f\left( 0 \right)\]
* Đáp án
C
* Hướng dẫn giải
Phương pháp giải: - Biến đổi bất phương trình về dạng \[m > g\left( x \right)\].
- Bất phương trình có nghiệm với mọi \[x \in (0;2) \Leftrightarrow m \ge \mathop {max}\limits_{[0;2]} g(x)\]
Giải chi tiết:
Ta có : \[f(x) < 2x + m \Leftrightarrow f(x) - 2x < m,\forall x \in (0;2)\]
\[ \Leftrightarrow m \ge \mathop {max}\limits_{[0;2]} [f(x) - 2x] = \mathop {max}\limits_{[0;2]} g(x)\]
Ở đó \[g(x) = f(x) - 2x \Rightarrow g\prime (x) = f\prime (x) - 2\].
Quan sát đồ thị hàm số \[y = f'\left( x \right)\] ta thấy \[f\prime (x) < 2,\forall x \in (0;2) \Rightarrow f\prime (x) - 2 < 0,\forall x \in (0;2)\]
\[ \Rightarrow g\prime (x) < 0,\forall x \in (0;2)\] hay hàm số \[y = g(x)\] nghịch biến trên đoạn
\[ \Rightarrow g(x) \le g(0) = f(0)\].
Do đó \[m \ge \mathop {max}\limits_{[0;2]} g(x) = f(0).\].
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
