Cho hàm số y = -x^3 + x^2 + (4m+9)x -5 (1) với m là tham số. Hỏi có bao nhiêu giá trị nguyên của

* Hướng dẫn giải

Phương pháp giải: - Tìm đạo hàm của hàm số.

- Cô lập m, đưa bất phương trình về dạng \[m \le f(x)\forall x \in (a;b) \Leftrightarrow m \le \mathop {min}\limits_{[a;b]} f(x)\].

- Lập BBT của hàm số \[f(x)\] và kết luận.

Giải chi tiết:

Ta có hàm số $y=\mathrm{ }-x^3+x^2+(4m+9)x-5$ nghịch biến trên khoảng $(-\mathrm{\infty };0)$ khi

$y\text{'}=-3x^2+2x+4m+9\le 0\forall x\in (-\mathrm{\infty };0)$

\[ \Leftrightarrow 4m \le 3{x^2} - 2x - 9\left( * \right)\]

Đặt \[f\left( x \right) = 3{x^2} - 2x - 9\]\[ \Rightarrow f'\left( x \right) = 6x - 2 = 0 \Leftrightarrow x = \frac{1}{3}\]

Bảng biến thiên:

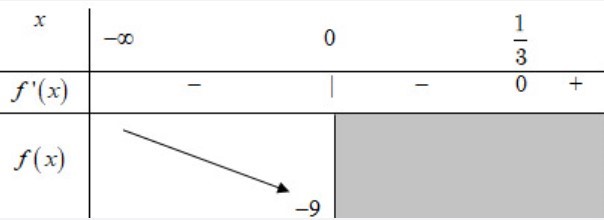
Dựa vào bảng biến thiên ta thấy bất phương trình (*) xảy ra khi $4m\le \mathrm{ }-9\iff m\le \mathrm{ }-94$

Kết hợp điều kiện $m>\mathrm{ }-10$nên $-10<m\le -94$. Mà $m\in Z\Rightarrow m\in \{-9;-8;\mathrm{\dots };-3\}$.

Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán.

Chọn B.