Trong không gian cho tam giác OIM vuông tại I góc IOM = 30^0 và IM = a. Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay có diệ...

Phương pháp giải: - Khi quay tam giác vuông IOM quanh cạnh góc vuông OI ta được một hình nón có chiều cao bằng độ dài cạnh OI và bán kính đáy là cạnh IM, đường sinh là cạnh huyền OM.

- Diện tích toàn phần của hình nón có độ dài đường sinh bằng \(l\) và bán kính đáy bằng \(r\) là \({S_{tp}}\, = \,\pi rl\, + \,\pi {r^2}\).

Giải chi tiết:

Khi quay tam giác vuông IOM quanh cạnh góc vuông OI ta được một hình nón có chiều cao bằng độ dài cạnh OI và bán kính đáy là cạnh IM, đường sinh là cạnh huyền OM. (như hình vẽ dưới đây)

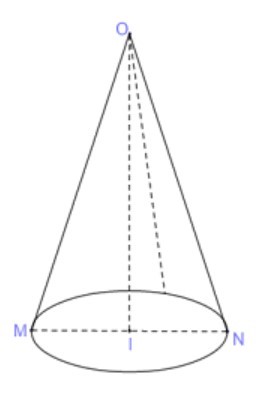
Tam giác OIM vuông tại I có \(\widehat {IOM} = 30^\circ ;IM = a\) nên ta có:

\[r = IM = a;\;l = OM = \frac{{IM}}{{sinIOM}} = \frac{a}{{sin30}} = 2a\]

Do đó diện tích toàn phần của hình nón tạo thành là:

      \[Stp = \pi rl + \pi {r^2} = \pi .a.2a + \pi {a^2} = 3\pi {a^2}\]

Chọn D.