Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông cân A BC = 2a. Góc giữa (AB'C) và (BB'C) bằng 60^0. Tính thể tích khối lăng trụ ABC.A'B'C'

Phương pháp giải: - Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Sử dụng tỉ số lượng giác của các góc nhọn trong tam giác vuông và hệ thức lượng trong tam giác vuông để tính chiều cao của khối lăng trụ.

- Khối lăng trụ có chiều cao \[h\], diện tích đáy B có thể tích là \[V = B.h\].

Giải chi tiết:

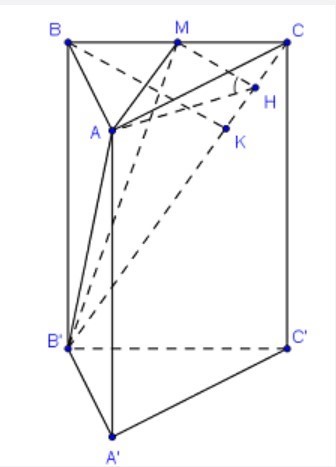
Gọi M là trung điểm của BC. Do ΔABC cân tại A nên \[AM \bot BC\]

Mà $AM\perp BB\text{'}\mathrm{ }\Rightarrow AM\perp (BB\text{'}C)$

Kẻ \[MH \bot B'C,BK \bot B'C \Rightarrow \angle MHA = \left( {\left( {BB'C} \right);\left( {AB'C} \right)} \right) = 60^\circ \]

Tam giác ABC vuông cân tại A \[ \Rightarrow AM = \frac{{BC}}{2} = \frac{{2a}}{2} = a\]

Tam giác AMH vuông tại M, \[\angle MHA = 60^\circ \; \Rightarrow MH = \frac{{AM}}{{tan60^\circ }} = \frac{a}{{\sqrt 3 }}\]

\[ \Rightarrow BK = 2.\frac{a}{{\sqrt 3 }} = \frac{{2a}}{{\sqrt 3 }}\]

Tam giác BB’C vuông tại B, BK là đường cao

 $$\begin{gathered} \begin{array}{c}\Rightarrow \frac{1}{B{K}^2}=\frac{1}{B{C}^2}+\frac{1}{B{B}^{\text{'}}2}\iff \frac{1}{{\left(\frac{2a}{\sqrt{3}}\right)}^2}=\frac{1}{{(2a)}^2}+\frac{1}{BB{\text{'}}^2}\end{array} \\ \Rightarrow B{B}^{\text{'}}=a\sqrt{2}\Rightarrow V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{ABC}.B{B}^{\text{'}}=(\frac{1}{2}.a.2a).a\sqrt{2}\mathrm{ }=a^3\sqrt{2}. \end{gathered}$$

Chọn B.