Cho hàm số y = f(x) có đạo hàm f(x) liên tục trên R và đồ thị hàm số
Câu hỏi :
Cho hàm số \[y = f(x)\] có đạo hàm \[f(x)\] liên tục trên R và đồ thị hàm số \[y = f(x)\] như hình vẽ.
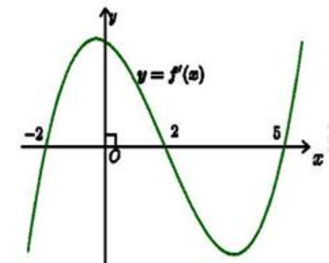
Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số \[y = f(\left| {x + 1} \right| - m)\] có 3 điểm cực trị. Tổng tất cả các phần tử của tập hợp S bằng ?
Cho hàm số \[y = f(x)\] có đạo hàm \[f(x)\] liên tục trên R và đồ thị hàm số \[y = f(x)\] như hình vẽ.

Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số \[y = f(\left| {x + 1} \right| - m)\] có 3 điểm cực trị. Tổng tất cả các phần tử của tập hợp S bằng ?
* Đáp án
B
* Hướng dẫn giải
Phương pháp giải: Hàm số \[y = f\left( {\left| x \right|} \right)\] có \[2a + 1\] điểm cực trị khi hàm số \[y = f\left( x \right)\] có \[a\] điểm cực trị dương.
Giải chi tiết:
Hàm số \[y = f\left( x \right)\] có 3 điểm cực trị là \[ - 2,{\mkern 1mu} {\mkern 1mu} 2,{\mkern 1mu} {\mkern 1mu} 5\].
Nên hàm số \[y = f\left( {\left( {x + 1} \right) - m} \right)\] có 3 điểm cực trị là
Hàm số \[y = f\left( {\left( {\left| {x + 1} \right|} \right) - m} \right)\] có đúng 3 điểm cực trị khi \[y = f\left( {\left( {x + 1} \right) - m} \right)\] có đúng 1 cực trị lớn hơn \[ - 1\].
Do đó Mà \[m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 4; - 3; - 2} \right\}\]
Vậy
Chọn B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
