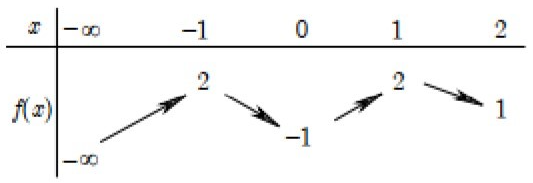
Cho hàm số y = f(x) liên tục trên tập xác định ( - vô cùng ;2] và bảng biến thiên như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f(x) = m có đúng hai nghiệm phân biệt

Đáp án: 2

Phương pháp giải: Số nghiệm của phương trình \[f\left( x \right) = m\] là số giao điểm của đồ thị hàm số \[y = f\left( x \right)\] và đường thẳng \[y = m\] song song với trục hoành.

Giải chi tiết:

Đường thẳng \[y = m\] cắt đồ thị hàm số \[y = f\left( x \right)\] tại 2 điểm phân biệt trên \[\left( { - \infty ;2} \right]\] khi và chỉ khi $[\begin{array}{c}m=\mathrm{ }-1\\ m=2\end{array}$.

Vậy có 2 giá trị của \[m\] thỏa mãn.