Có bao nhiêu số phức z thỏa mãn |z|^2 = 2|z + z| + 4 và

* Hướng dẫn giải

Đáp án: 3

Phương pháp giải: +) Gọi số phức $z=a+bi\Rightarrow \overline{z}\mathrm{ }=a-bi$.

+) Từ mỗi giải thiết đã cho, tìm đường biểu diễn số phức z.

+) Tìm giao điểm của đường biểu diễn số phức z ở giả thiết thứ nhất và thứ 2.

Giải chi tiết:

Gọi số phức $z=a+bi\Rightarrow \overline{z}\mathrm{ }=a-bi$.

Từ giả thiết thứ nhất ta có :

$|z{|}^2=2|z+\overline{z}|+4\iff a^2+b^2-2.2|a|-4=0\iff [\begin{array}{c}{a}^2+b^2-4a-4=0\{a^2+b^2+4a-4=0\end{array}$

⇒ Tập hợp các số phức z là đường tròn \[\left( {{C_1}} \right):{x^2} + {y^2} - 4x - 4 = 0\;\] hoặc \[\left( {{C_2}} \right):{x^2} + {y^2} + 4x - 4 = 0.\]

Từ giả thiết thứ hai ta có:

$\begin{array}{c}|z-1-i|=|z-3+3i|\iff |a-1+bi-i|=|a-3+bi+3i|\\ \iff {(a-1)}^2+{(b-1)}^2={(a-3)}^2+{(b+3)}^2\\ \iff \mathrm{ }-2a+1-2b+1=\mathrm{ }-6a+9+6b+9\\ \iff 4a-8b-16=0\iff a-2b-4=0\end{array}$

⇒ Tập hợp các số phức z là đường thẳng \[x - 2y - 4 = 0\left( d \right).\]

Vậy số phức thỏa mãn 2 giả thiết trên là số giao điểm của d với \[\left( {{C_1}} \right)\] và \[\left( d \right)\] với \[\left( {{C_2}} \right)\].

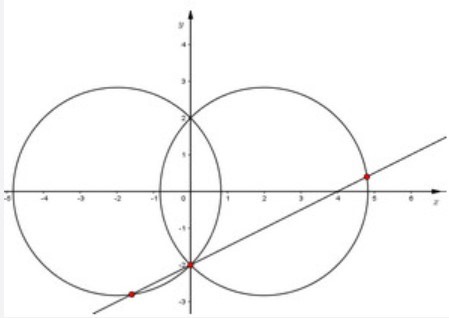
Dựa vào hình vẽ ta thấy có 3 giao điểm của d với \[\left( {{C_1}} \right)\] và \[\left( d \right)\] với \[\left( {{C_2}} \right)\]. Vậy có 3 số phức thỏa mãn yêu cầu bài toán.