Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a, cạnh bên bằng a. Góc giữa hai mặt phẳng (ABC') và (ABC) bằng
Câu hỏi :
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a, cạnh bên bằng a. Góc giữa hai mặt phẳng (ABC') và (ABC) bằng
* Đáp án
* Hướng dẫn giải
Đáp án:30
Phương pháp giải: Góc giữa hai mặt phẳng (khác \[90^\circ \]) bằng góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.
Giải chi tiết:
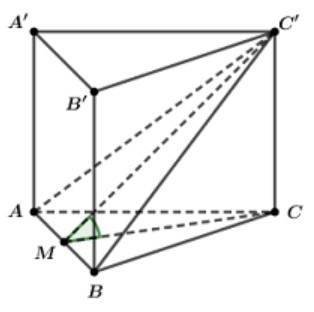
Gọi \[M\] là trung điểm của \[AB\]
\[ \Rightarrow \left\{ \begin{array}{l}CM \bot AB\\C'M \bot AB\end{array} \right. \Rightarrow \left( {(AB\widehat {C),(A}BC')} \right) = \left( {C\widehat {M,C'}M} \right) = \widehat {CMC'}\]
Tam giác \[ABC\] đều cạnh 2a nên \[CM = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \]
Tam giác vuông tại C nên :
\(\tan \widehat {CC'M} = \frac{{CC'}}{{CM}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {CMC'} = 30^\circ \)
Vậy \[\left( {(AB\widehat {C),(A}BC')} \right) = 30^\circ \].
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
