Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác ABC vuông tại A với AC = a. Biết hình chiếu vuông góc của B' lên (ABC) là trung điểm H của BC. Mặt phẳng

* Hướng dẫn giải

Đáp án:.\(\frac{{\sqrt 3 a}}{3}\) 

Giải chi tiết:

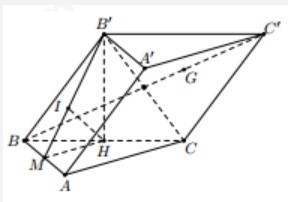
Gọi M là trung điểm của AB. Khi đó \[HM \bot AB\], suy ra \[AB \bot \left( {AHM} \right)\], do đó:

\(\widehat {B'MH} = \left( {(ABB'\widehat {A');(A}BC)} \right) = 60^\circ \)

Gọi I là hình chiếu của H trên \(B'M\). Khi đó \[HI \bot AB\] nên \[HI \bot \left( {ABB'A'} \right)\]. Ta có:

\[d(G;\left( {ABB'A'} \right) = \frac{2}{3}d(C';\left( {ABB'A'} \right) = \frac{2}{3}d\left( {C;\left( {ABB'A'} \right)} \right) = \frac{4}{3}d\left( {H;\left( {ABB'A\prime '} \right)} \right) = \frac{4}{3}HI\]

Xét tam giác vuông \[B'HM\], ta có $MH=\frac{AC}{2};B^{\text{'}}H=HM.tan{60}^{\circ }\mathrm{ }=\frac{a\sqrt{3}}{2}$.

Vậy \[d(G;\left( {ABB'A'} \right) = \frac{{4HI}}{3} = \frac{{4HM.HB'}}{{3\sqrt {H{M^2} + HB{'^2}} }} = \frac{{a\sqrt 3 }}{3}\].