Tập nghiệm của bất phương trình (2x+1)/(2x^2-3x_1)>=0

Phương pháp giải: Lập bảng xét dấu, giải bất phương trình

Giải chi tiết:

\(\frac{{2x}}{{2{x^2} - 3x + 1}} \ge 0 \Leftrightarrow \frac{{2x + 1}}{{(2x - 1)(x + 1)}} \ge 0\)                 ĐKXĐ: \(\left\{ {\begin{array}{*{20}{c}}{x \ne 1}\\{x \ne \frac{1}{2}}\end{array}} \right.\)

Đặt \(f(x) = \frac{{2x}}{{2{x^2} - 3x + 1}}\). Ta có bảng:

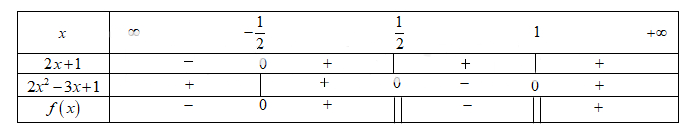
Vậy \(f\left( x \right)\, \ge \,0\, \Leftrightarrow \,x\, \in \,\left[ { - \frac{1}{2}\,;\,\frac{1}{2}} \right]\, \cup \,\left( {1\,;\, + \infty } \right)\)

Chọn B.