Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a , hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) là trung điểm của AB. Mặt bên

Phương pháp giải: - Xác định góc giữa hai mặt phẳng \[\left( {ACC'A'} \right)\] và \[\left( {ABC} \right)\] Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính chiều cao và diện tích đáy của lăng trụ.

- Sử dụng công thức tính thể tích lăng trụ: \[{V_{lt}} = \,{S_{day}}.\,h\] trong đó \[{S_{day}}\] và \[h\] lần lượt là diện tích đáy và chiều cao của lăng trụ

Giải chi tiết:

Gọi \[D,E\]lần lượt là trung điểm \[AB,AC\]

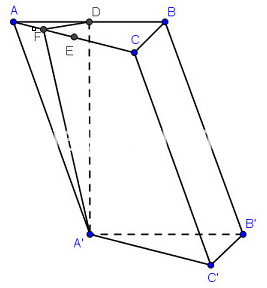
Vì tam giác \[ABC\]đều cạnh \[a\] nên \[BE \bot AC\]và  \[BE = \frac{{a\sqrt 3 }}{2},{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\]

Gọi \[F\]là điểm trên cạnh \[AC\]sao cho \[F\]là trung điểm \[AE\]ta có: 

\[DF//BE\] (do \[DF\]là đường trung bình của tam giác \[ABE\]) mà \[BE \bot AC\]nên \[DF \bot AC\].

Ta có: \[\left\{ {\begin{array}{*{20}{c}}{AC \bot DF}\\{AC \bot A'D(A'D \bot (ABC))}\end{array} \Rightarrow AC \bot (DFA') \Rightarrow AC \bot A'F} \right.\]

Ta có: \[\left\{ {\begin{array}{*{20}{c}}{\left( {ACC'A'} \right) \cap \left( {ABC} \right) = AC}\\{\left( {ACC'A'} \right) \supset A'F \bot AC}\\{\left( {ABC} \right) \supset \,DF\, \bot \,AC}\end{array}} \right. \Rightarrow \angle \,\left( {\left( {ACC'A'} \right)\,;\,\left( {ABC} \right)} \right) = \,\angle \left( {A'F;DE} \right)\]

\[ \Rightarrow \angle DFA' = 45^\circ \, \Rightarrow \,\Delta DFA'\] vuông cân tại \[D\]

\[ \Rightarrow A'D = DF = \frac{1}{2}BE = \frac{1}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4}\]

\[ \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.A'D = \frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 3 }}{4} = \frac{{3{a^3}}}{{16}}\]

Chọn B.