Cho hình chóp S.ABC có đáy ABC là tam giác vuông với AB = AC = 2. Cạnh bên SA vuông góc với đáy và SA = 3. Gọi M là trung điểm của SC. Tính khoảng cách giữa AM và BC.
Câu hỏi :
Cho hình chóp S.ABC có đáy ABC là tam giác vuông với \(AB\, = \,AC\, = \,2\). Cạnh bên SA vuông góc với đáy và \(SA\, = \,3\). Gọi \(M\)là trung điểm của SC.
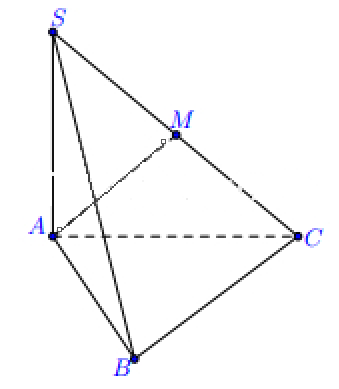
Tính khoảng cách giữa AM và BC.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông với \(AB\, = \,AC\, = \,2\). Cạnh bên SA vuông góc với đáy và \(SA\, = \,3\). Gọi \(M\)là trung điểm của SC.

Tính khoảng cách giữa AM và BC.
A. \(d\left( {AM\,;\,BC} \right)\, = \,\frac{{\sqrt 3 }}{2}\)
* Đáp án
C
* Hướng dẫn giải
Phương pháp giải: - Sử dụng: khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường này đến mặt phẳng song song chứa đường thẳng kia
- Sử dụng: \({\left[ {\left( {\frac{1}{{{{(x - 1)}^2}}}} \right)} \right]^\prime }\) \(d\left( {S\,;\,\left( {AMN} \right)} \right) = \frac{{3{V_{S.AMN}}}}{{{S_{\Delta AMN}}}}\)
Giải chi tiết:
Gọi N là trung điểm của BC ta có MN // BC \( \Rightarrow \)BC // (AMN) \( \supset \)AM
\( \Rightarrow \)d (AM; BC) = d (BC; (AMN)) = d (C; (AMN))
Lại có: SC \( \cap \) (AMN) = M \( \Rightarrow \) \(\frac{{d(C;(AMN))}}{{d(S;(AMN))}} = \frac{{CM}}{{SM}} = 1\)
\( \Rightarrow d(C;(AMN)) = d(S;(AMN))\)
Ta có:
Gọi p là nửa chu vi tam giác AMN ta có
Vậy \( \Rightarrow d(AM;BC) = d(S;(AMN)) = \frac{{3{V_{S.AMN}}}}{{{S_{\Delta AMN}}}} = \frac{{3.\frac{1}{2}}}{{\frac{{\sqrt {22} }}{4}}} = \frac{{3\sqrt {22} }}{{11}}\)
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
