Cho hàm số y = f(x) có đạo hàm trên R là f'( x ) = (x^2 - 3x)( x^3 - 4). Điểm cực đại của hàm số đã cho là:

* Hướng dẫn giải

Đáp án: x=2

Phương pháp giải:  Ta có: \(x = {x_0}\)là điểm cực trị của hàm số \(y = f(x)\)\( \Rightarrow f'({x_0}) = 0\)

Điểm \(x = {x_0}\)là điểm cực đại của hàm số \(y = f(x)\)\( \Leftrightarrow \)tại điểm \(x = {x_0}\)thì hàm số có\(y'\)đổi dấu từ dương sang âm

Lập bảng xét dấu của hàm số rồi chọn đáp án đúng

Giải chi tiết:

Ta có:  \(f'(x) = 0\)

$\begin{array}{c}\iff (x^2-3x)(x^3-4x)=0\iff x^2(x-3)(x^2-4)=0\iff [\begin{array}{c}x=0\\ x-3=0\\ x^2-4=0\end{array}\iff [\begin{array}{c}x=0\\ x=3\\ x=-2\end{array}\end{array}$

Lập bảng xét dấu:

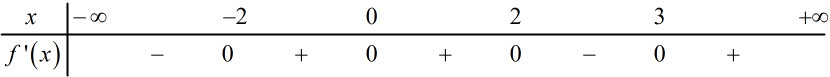
Dựa vào bảng xét dấu ta có: qua điểm \(x = 2\)thì \(f'(x)\)đổi dấu từ \( + \)sang \( - \)nên \(x = 2\)là điểm cực đại của hàm số

\( \Rightarrow \) hàm số có 1 điểm cực đại là \(x = 2\)