Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ toạ độ Oxy
Câu hỏi :
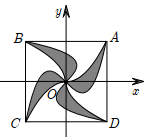
Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ toạ độ Oxy với \(O\)là tâm hình vuông sao cho\(A\left( {1\,;\,1} \right)\) như hình vẽ bên thì các đường cong OA có phương trình \(y\, = \,{x^2}\) và \(y\, = \,a{x^3}\, + \,bx\). Tính giá trị ab biết rằng diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\) diện tích mặt sàn.

* Đáp án
* Hướng dẫn giải
Đáp án: -2
Phương pháp giải: - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x),y = g(x)\), đường thẳng\(x = a,x = b\)là \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \). Từ đó tính diện tích 1 cánh của hình trang trí và suy ra diện tích hình trang trí
- Sử dụng dữ kiện diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\)diện tích mặt sàn suy ra 1 phương trình bậc nhất 2 ẩn\(a,b\)
- Sử dụng đồ thị hàm số \(y = a{x^3} + bx\)đi qua điểm \(A(1;1)\)suy ra thêm 1 phương trình bậc nhất 2 ẩn \(a,b\)
- Giải hệ tìm \(a,b\)và tính\(ab\)
Giải chi tiết:
Diện tích 1 cánh của hình trang trí là:
\( \Rightarrow \)diện tích hình trang trí là: \(S = 4{S_1} = \frac{4}{3} - a - 2b\)
Vì diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\)diện tích mặt sàn nên
Khi đó ta có:
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
